Class 8 Maths Ganita Prakash Chapter 4 Quadrilaterals NCERT Solutions
Text Book Page 94
Question 1: Find all the other angles inside the following rectangles
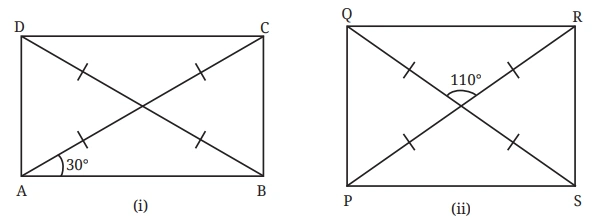
Solution:-
Question 2: Draw a quadrilateral whose diagonals have equal lengths of 8 cm that bisect each other, and intersect at an angle of
(i) 30° (ii) 40° (iii) 90° (iv) 140°
Solution:
Question 3: Consider a circle with centre O. Line segments PL and AM are two perpendicular diameters of the circle. What is the figure APML? Reason and/or experiment to figure this out.
Solution:
Question 4: We have seen how to get 90° using paper folding. Now, suppose we do not have any paper but two sticks of equal length, and a thread. How do we make an exact 90° using these?
Solution:
Question 5: We saw that one of the properties of a rectangle is that its opposite sides are parallel. Can this be chosen as a definition of a rectangle? In other words, is every quadrilateral that has opposite sides parallel and equal, a rectangle?
Solution:
Figure It Out (Page 102)
Question 1: Find the remaining angles in the following quadrilaterals.
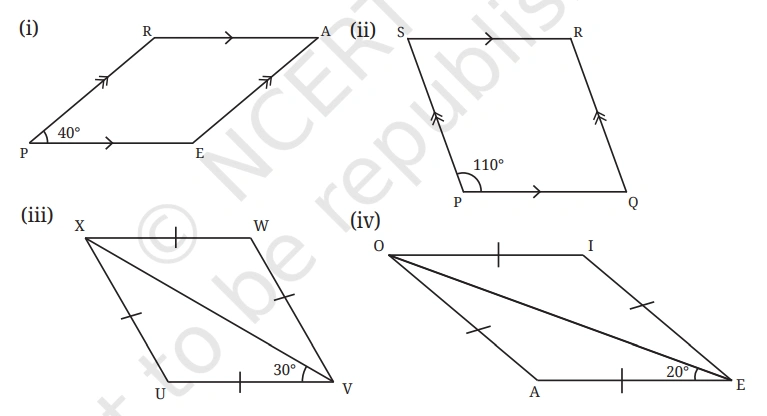
Solution:
Question 2: Using the diagonal properties, construct a parallelogram whose diagonals are of lengths 7 cm and 5 cm, and intersect at an angle of 140°.
Solution:
Question 3: Using the diagonal properties, construct a rhombus whose diagonals are of lengths 4 cm and 5 cm.
Solution:
4.5 Playing with Quadrilaterals, 4.6 Kite and Trapezium
Figure It Out (Pages 107-109)
Question 1: Find all the sides and the angles of the quadrilateral obtained by joining two equilateral triangles with sides 4 cm.
Solution:
Question 2: Construct a kite whose diagonals are of lengths 6 cm and 8 cm.
Solution:
Question 3: Find the remaining angles in the following trapeziums—
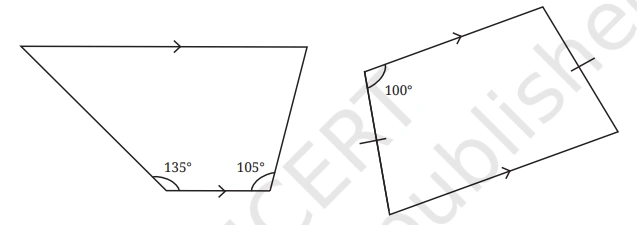
Solution:
Question 4: Draw a Venn diagram showing the set of parallelograms, kites, rhombuses, rectangles, and squares. Then, answer the following questions—
(i) What is the quadrilateral that is both a kite and a
parallelogram?
(ii) Can there be a quadrilateral that is both a kite and a rectangle?
(iii) Is every kite a rhombus? If not, what is the correct relationship between these two types of quadrilaterals?
Solution:
Question 5: If PAIR and RODS are two rectangles, find ∠IOD.
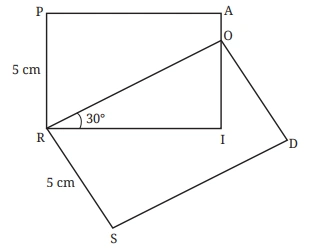
Solution:
Question 6: Construct a square with diagonal 6 cm without using a protractor.
Solution:
Quetsion 7: CASE is a square. The points U, V, W and X are the midpoints of the sides of the square. What type of quadrilateral is UVWX? Find this by using geometric reasoning, as well as by construction and measurement. Find other ways of constructing a square within a square such that the vertices of the inner square lie on the sides of the outer square, as shown in Figure (b).
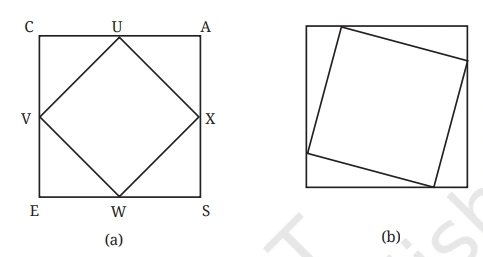
Solution:
Question 8: If a quadrilateral has four equal sides and one angle of 90°, will it be a square? Find the answer using geometric reasoning as well as by construction and measurement.
Solution:
Question 9: What type of a quadrilateral is one in which the opposite sides are equal? Justify your answer.
Hint: Draw a diagonal and check for congruent triangles.
Solution:
Question 10: Will the sum of the angles in a quadrilateral such as the following one also be 360°? Find the answer using geometric reasoning as well as by constructing this figure and measuring
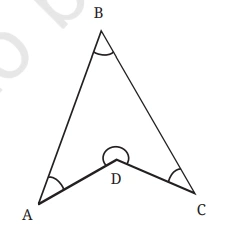
Solution:
Question 11: State whether the following statements are true or false. Justify your
answers.
(i) A quadrilateral whose diagonals are equal and bisect each other must be a square.
(ii) A quadrilateral having three right angles must be a rectangle.
(iii) A quadrilateral whose diagonals bisect each other must be a parallelogram.
(iv) A quadrilateral whose diagonals are perpendicular to each other must be a rhombus.
(v) A quadrilateral in which the opposite angles are equal must be a parallelogram.
(vi) A quadrilateral in which all the angles are equal is a rectangle.
(vii) Isosceles trapeziums are parallelograms.
Solution:-