Large Numbers Around Us Class 7 Solutions Ganita Prakash Maths Chapter 1
Class 7 Maths Ganita Prakash Chapter 1 Large Numbers Around Us NCERT Solutions provide you the best study material available online, covering the exercises and questions of Chapter 1 Large Numbers Around Us.
NCERT Class 7 Maths Chapter 1 Large Numbers Around Us Solutions Question Answer
Ganita Prakash Class 7 Chapter 1 Solutions Large Numbers Around Us
NCERT Class 7 Maths Ganita Prakash Chapter 1 Large Numbers Around Us Solutions Question Answer
NCERT Text Question Page (1 – 2)
Question 1. Eshwarappa is a farmer in Chintamani, a town in Karnataka. He visits the market regularly to buy seeds for his rice field. During one such visit he overheard a conversation between Ramanna and Lakshmamma. Ramanna said, “Earlier our country had about a lakh varieties of rice. Farmers used to preserve different varieties of seeds and use them to grow rice. Now, we only have a handful of varieties. Also, farmers have to come to the market to buy seeds”. Lakshmamma said, “There is a seed bank near my house. So far, they have collected about a hundred indigenous varieties of rice seeds from different places. You can also buy seeds from there.”
Eshwarappa shared this incident with his daughter Roxie and son Estu . Estu was surprised to know that there were about one lakh varieties of rice in this country. He wondered “One lakh! So far I have only tasted 3 varieties. If we tried a new variety each day, would we even come close to tasting all the varieties in a lifetime of 100 years?” What do you think? Guess.

Solution:-
🧁 Can Roxie and Estu Taste All 1,00,000 Varieties?
Let’s find out with a little math magic! ✨
📌 Given:
- Total varieties = 1,00,000
- Varieties tasted per day = 1
- Days in a year = 365
🧮 Step-by-Step Calculation
Step 1: How many varieties can they taste in 1 year?
[ 1 variety a day x 365 days in a year} = 365 varieties per year ]
Step 2: How many years to taste all 1,00,000 varieties?
[ 1,00,000 varieties ÷ 365 varieties per year = approx 274 years ]
😲 What Does This Mean?
Even if Roxie and Estu taste one new variety every single day, it would take them 274 years to finish all of them!
But most people live around 70–80 years, so… They won’t be able to taste every single one in their lifetime.
Q. 2. But how much is one lakh? Observe the pattern and fill in the boxes given below.
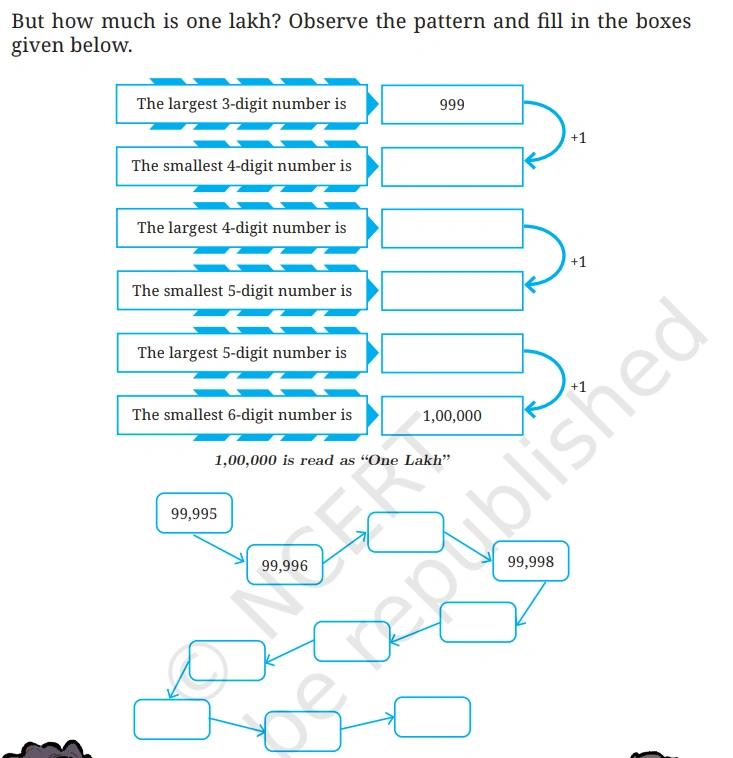
Solution:-
Q. 3. Roxie and Estu found that if they ate one variety of rice a day, they would come nowhere close to a lakh in a lifetime! Roxie suggests, “What if we ate 2 varieties of rice every day? Would we then be able to eat 1 lakh varieties of rice in 100 years?”

Solution:-
Q. 4 What if a person ate 3 varieties of rice every day? Will they be able to taste all the lakh varieties in a 100 year lifetime? Find out.
Solution:-
NCERT Text Question Page – 3
Q. 5. Estu said, “We know how many day there are in a year – 365, if we ignore leap years. If we live for y years, the number of days in our lifetime will be 365 x y.”
Choose a number for y. How close to one lakh is the number of days in y years, for the y of your choice?
Solution:-
Figure it out
Q. 1. According to the 2022 Census, the population of the town of Chintamani was about 75,000. How much less than one lakh is 75,000?
Solution:-
Q. 2. The estimated population of Chintamani in the year 2024 is 1,06,000. How much more than one lakh is 1,06,000?
Solution:-
Q.3. By how much did the population of Chintamani increase from 2022 to 2024?
Solution:-
Getting a Feel of Large Numbers
You may have come across intersecting facts like these:
The world’s tallest statue is the ‘Statue of Unity‘ in Gujarat depicting Sardar Vallabhbhai Patel. Its height is about 180 meteres.
Kunchikal Waterfall in Karnataka is said to drop from a height of about 450 metres.
Loot at the picture on the right. Somu is 1 metre tall. If each floor is about four times his height, what is the approximate height of the building?
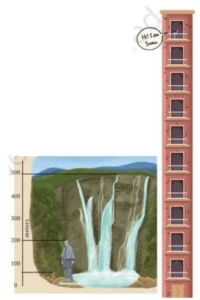
Q. 1. Which is taller – The Statue of Unity or this building? How much taller? __ m.
Solution:-
Q. 2. How much taller is the kunchikal waterfall than Somu’s building? __ m.
Solution:-
Q. 3. How many floor should Somun’s Building have to be as high as the waterfall?
Solution:-
NCERT Text Questions (Page – 4)
Is one Lakh a Very Large Number?
Q. How do you view a lakh – is a lakh big or small?
Solution:-
NCERT Text Question (Pages 4 – 5)
Reading and Writing Numbers:
Q. Write each of the numbers give below in words:
(a) 3,00,600
(b) 5,04,085
(c) 27,30,000
(d) 70,53,138
Solution:-
Q. Write the corresponding number in the Indian place value system for each of the following:
(a) One lakh twenty three thousand four hundred and fifty six
(b) Four lakh seven thousand seven hundred and four
(c) Fifty lakhs five thousand and fifty
(d) Ten lakhs two hundred and thirty five
Solution:-
NCERT Text Question (Pages 4 – 5)
1.2 Land of Tens
In the Land of Tens, there are special calculators with special buttons.
Q. 1. The Thoughtful Thousands only has a -1000 button. How many times should it be pressed to show:
(a) Three thousand? 3 times
(b) 10,000?
(c) Fifty three thousand?
(d) 90,000? __
(e) One Lakh? ____
(f) __? 153 times
(g) How many thousands are required to make one lakh?
Solution:-
Q. 2. The Tedious Tens only has a +10 button. How many times should it be pressed to show:
(a) Five hundred? _
(b) 780?
(c) 1000?
(d) 3700?
(e) 10,000?
(f) One lakh?_
(g) __? 435 times
Solution:-
Q. 3. The Handy Hundreds only has a +100 button. How many times should it be pressed to show:
(a) Four hundred? times
(b) 3,700?
(c) 10,000?
(d) Fifty three thousand?
(e) 90,000? _
(f) 97,600?
(g) 1,00,000?
(h) __? 582 times
(I) How many hundreds are required to make ten thousand?
(j) How many hundreds are required to make one lakh?
(k) Handy Hundreds says, “There are some numbers which Tedious Tens and Thoughtful Thousands can’t show but I can.” Is this statement true? Think and explore.
Solution:-
Q. 4. Creative Chitti is a different kind of calculator. It has the following buttons:
+1, +10, +100, +1000, +10,000, +100000and +1000000. It always has multiple ways of doing things. “How so?’, you might ask. To get the number 321, it presses +10 thirty two times and +1 once. Will it get 321? Alternatively, it can press +100 two times and +10 twelve times and +1 once.
Solution:-
Q. 5. Two of the many different ways to get 5072 are shown below. These two ways can be expressed as:
(a) (50 x 100) + (7 x 10) + (2 x 1) = 5072
(b) (3 x 1000) + (20 x 100) + (72 x 1) = 5072
Q. Find a differenct way to get 5072 and write an expression for the same.
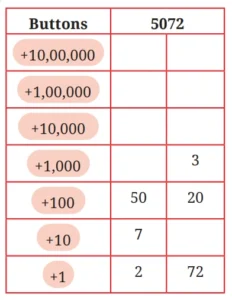
Solution:-
NCERT Text Question Page (7)
Figure it Out
Q. 1. For the numbers in the previous exercise, find out how to get each number by making the smallest number of button clicks and write the expression.
Solution:-
Q. 2. Do you see any connection between each number and the corresponding smallest number of button clicks?
Solution:-
Q. 3. If you notice, the expressions for the least button clicks also give the Indian place value notation of the numbers. Think about why this is so.
What if we press the +10,00,000 button ten times? What number will come up? How many zeros will it have? What should we call it? The number will be 100 lakhs, which is also called a crore. 1 crore is written as 1,00,00,000 – it is 1 followed by seven zeroes.
Solution:-
NCERT Question Page (8-9)
Figure it out
Q. 1. How many zeros does a thousand lakh have? –
Solution:-
How many zeros does a hundred thousand have? –
Solution:-
NCERT Question Page (9)
Figure it Out
Q. 1. Read the following numbers in Indian Place value notation and write their number names in both the Indian and American systems:
(a) 4050678
(b) 48121620
(c) 20022002
(d) 246813579
(e) 345000543
(f) 1020304050
Solution:-
Q. 2. Write the following numbers in Indian place value notation:
(a) one crore one lakh one thousand ten
(b) One billion one million one thousand one
(c) Ten crore twenty lakh thirty thousand forty
(d) Nine billion eighty million seven hundred thousand six hundred
Solution:-
Q. 3. Compare and write ‘<‘, ‘>’ or ‘=’.
(a) 30 thousand __ 3 lakhs
(b) 500 lakhs _ 5 million
(c) 800 thousand_____8 million
(d) 640 crore______60 billion
Solution:-
1.4 Exact and Approximate Values
NCERT Question Page (10)
Q. Think and share situations where it is appropriate to (a) round up, (b) round down, (c) either rounding up or rounding down is okay and (d) when exact numbers are needed
Solution:-
NCERT Question Page (11)
Nearest Neighbours
Q. 1. Similarly, write the five nearest neighbours for these numbers:
(a) 3,87,69,957
(b) 29,05,32,481
Solution:-
Q. 2. I have a number for which all five nearest neighbours are 5,00,00,000. What could the number be? How many such numbers are there?
Solution:-
Roxie and Estu are estimating the values of simple expressions.
Queastion – 1
4,63,128 + 4,19,682,
Roxie: “The sum is near 8,00,000 and is more than 8,00,000.”
Estu: “The sum is near 9,00,000 and is less than 9,00,000.”
(a) Are these estimates correct? Whose estimate is closer to the sum?
(b) Will the sum be greater than 8,50,000 or less than 8,50,000? Why do you think so?
(c) Will the sum be greaterthan 8,83,128 or less than 8,83,128? Why do you think so?
(d) Exact value of 4,63,128 + 4,19,682 = __.
Question – 2
14,63,128 – 4,90,020
Roxie: “The difference is near 10,00,000 and is less than 10,00,000.”
Estu: “The difference is near 9,00,000 and is more than 9,00,000.”
(a) Are these estimates correct? Whose estimate is closer to the difference?
(b) Will the difference be greater than 9,50,000 or less than 9,50,000? Why do you think so?
(c) Will the difference be greater than 9,63,128 or less than 9,63,128? Why do you think so?
(d) Exact value of 14,63,128 – 4,90,020 = _
Solution:-
NCERT Text Question Page (13)
Population of the Cities
From the information given in the table, answer the following questions by approximation:
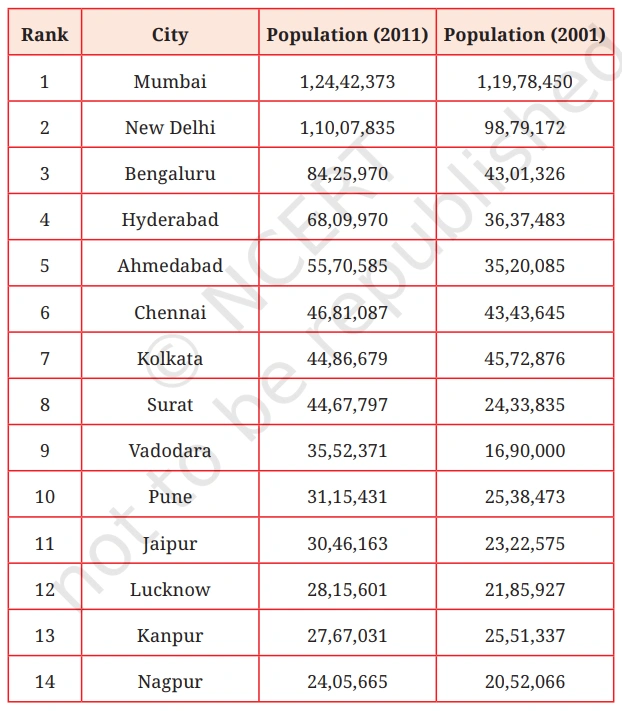
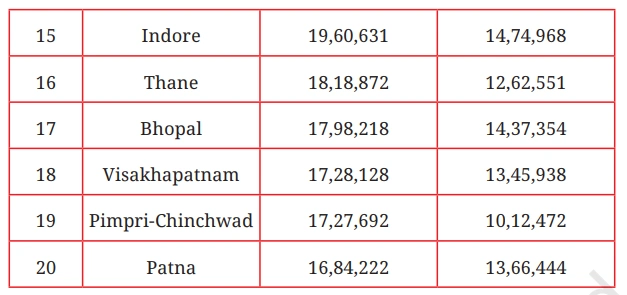
Q. 1. What is your general observation about this data? Share it with the class.
Solution:-
Q. 2. What is an appropriate title for the above table?
Solution:-
Q. 3. How much is the population of Pune in 2011? Approxiamtely, by how much has it increased compared to 2001?
Solution:-
Q. 4. Which cith’s population increased the most between 2001 and 2011?
Solution:-
Q. 5. Are there cities whose population has almost doubled? Which are they?
Solution:-
Q. 6. By what number should we multiply Patna’s population to get a number/population close to that of Mumbai?
Solution:-
1.5 Patterns in Products
A Multiplication Shortcut
NCERT In-Text Questions (page 14)
Q. using the meaning of multiplication and division, can you explain why multiplying by 5 is the same as dividing by 2 and multiplying by 10?
Solution:-
Figure it Out
Q. 1. Find quick ways to calculate these products:
(a) 2 x 1768 x 50
(b) 72 x 125 [Hint: 125 = 1000/8]
(c) 125 x 40 x 8 x 25
Q. 2. Calculate these products quickly.
(a) 25 x 12 =
(b) 25 x 240 =
(c) 250 x 120 =
(d) 2500 x 12 =
(e) _ x _ = 120000000
How Long is the product?
Q. In each of the following boxes, the multiplications produce interesting patterns. Evaluate them to find the pattern. Extend the multiplications based on the observed pattern.
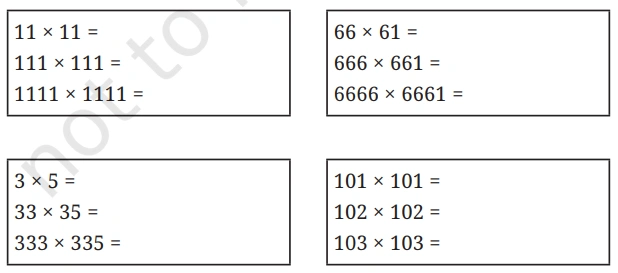
Solution:-
Q. Observe the number of digits in the two numbers being multiplied and their product in each case. Is there any connection between the numbers being multiplied and the number of digits in their product?
Solution:-
Q. Roxie says that the product of two 2-digit numbers can only be a 3- or a 4- digit number. Is She Correct?
Solution:-
Q. Should we try all possible multiplications with 2-digit numbers to tell whether Roxie’s claim is true? Or is there a better way to find out?
Solution:-
Q. Can multiplying a 3-digit number with another 3-digit number give a 4-digit number?
Solution:-
Q. Can multiplying a 4-digit number with a 2-digit number give a 5-digit number?
Solution:-
Q. Observe the multiplication statements below. Do you notice any patterns? See if this pattern extends for other numbers as well.

Solution:-
Did You Ever Wonder
NCERT In-Text Questions (Page 19)
Q. The RMS Titanic Ship carried about 2500 passengers. Can the population of Mumbai fit into 5000 such ships?

Solution:-
Q. Inspired by this strange question, Roxie wondered, “If I could travel 100 kilometers every day, could I reach the Moon in 10 years?’ (The distance between the Earth and the Moon is 3,84, 400 Km)
1 How far would she have travelled in a year?
2. How far would she have travelled in 10 years?
3. Is it not easier to perform these calculations in stages? You can use this method for all large calculations.
Solution:-
Q. Find out if you can reach the Sun in a lifetime, if you travel 1000 kilometers every day. (You had written down the distance between the Earth and the Sun in a previous exercise.)
Solution:-
Q. Make necessary reasonable assumptions and answer the questions below:
(a) If a single sheet of paper weighs 5 grams, could you lift one lakh sheets of paper together at the same time?
(b) If 250 babies are born every minute across the world, will a million babies be born in a day?
(c) Can you count 1 million coins in a day? Assume you can count 1 coin every second.
Solution:-
Q. Think and create more such fun questions and share them with your class.
Solution:-
NCERT Text Questions Page (19 – 20)
Figure it Out
Q. 1. Using all digits from 0 – 9 exactly once (the first digit cannot be 0) to create a 10-digit number, write the —.
(a) Largest multiple of 5
(b) Smallest even number
Solution:-
Q. 2. The number 10,30,285 in words is Ten lakhs thirty thousand two hundred eighty five, which has 43 letters. Give a 7-digit number name which has the maximum number of letters.
Solution:-
Q. 3. Write a 9-digit number where exchanging any two digits results in a bigger number. How many such numbers exist?
Solution:-
Q. 4. Strike out 10 digits from the number 12345123451234512345 so that the remaining number is as large as possible.
Solution:-
Q. 5. The words ‘zero’ and ‘one’ share letters ‘e’ and ‘o’. The words ‘one’ and ‘two’ share a letter ‘o’, and the words ‘two’ and ‘three’ also share a letter ‘t’. How far do you have to count to find two consecutive numbers which do not share an English letter in common?
Solution:-
Q. 6. Suppose you write down all the numbers 1, 2, 3, 4, …, 9, 10, 11, … The tenth digit you write is ‘1’ and the eleventh digit is ‘0’, as part of the number 10.
(a) What would the 1000th digit be? At which number would it occur?
(b) What number would contain the millionth digit?
(c) When would you have written the digit ‘5’ for the 5000th time?
Solution:-
Q. 7. A calculator has only ‘+10,000’ and ‘+100’ buttons. Write an expression describing the number of button clicks to be made for the following numbers:
(a) 20,800
(b) 92,100
(c) 1,20,500
(d) 65,30,000
(e) 70,25,700
Solution:-
Q. 8. How many lakhs make a billion?
Solution:-
Q. 9. You are given two sets of number cards numbered from 1 – 9. Place a number card in each box below to get the
(a) largest possible sum
(b) smallest possible difference of the two resulting numbers.
Solution:-
Q. 10. You are given some number cards; 4000, 13000, 300, 70000, 150000, 20, 5. Using the cards get as close as you can to the numbers below using any operation you want. Each card
can be used only once for making a particular number.
(a) 1,10,000: Closest I could make is 4000 × (20 + 5) + 13000 = 1,13,000
(b) 2,00,000:
(c) 5,80,000:
(d) 12,45,000:
(e) 20,90,800:
Solution:-
Q. 11. Find out how many coins should be stacked to match the height of the Statue of Unity. Assume each coin is 1 mm thick.
Solution:-
Q. 12. Grey-headed albatrosses have a roughly 7-feet wide wingspan. They are known to migrate across several oceans. Albatrosses can cover about 900 – 1000 km in a day. One of the longest single trips recorded is about 12,000 km. How many days would such a trip take to cross the Pacific Ocean approximately?
Solution:-
Q. 13. A bar-tailed godwit holds the record for the longest recorded non-stop flight. It travelled 13,560 km from Alaska to Australia without stopping. Its journey started on 13 October 2022 and continued for about 11 days. Find out the approximate distance it covered every day. Find out the approximate distance it covered every hour.
Solution:-
Q. 14. Bald eagles are known to fly as high as 4500 – 6000 m above the ground level. Mount Everest is about 8850 m high. Aeroplanes can fly as high as 10,000 – 12,800 m. How many times bigger are these heights compared to Somu’s building?
Solution:-