NCERT Class 7 Maths Ganita Prakash Chapter 2 Arithmetic Expressions Solutions

2.1 Simple Expressions

NCERT In-Text Question Page 24

Q. Example 1: Mallika spends ₹ 25 every day for lunch at school. Write the expression for the total amount she spends on lunch in a week from Monday to Friday.

Solution:-

Money spent every day = ₹ 25

The total amount spent from Monday to Friday = 5 x 25

Question: Choose your favourite number and write as many expressions as you
can having that value.

Solution:-

Let us choose the number 30.

We can write the arithmetic expressions for the number as follows:

12 + 18 = 30; 6 × 5 = 30; 60 ÷ 2 = 30, etc.

Figure it out (Page 25)

Question 1: Fill in the blanks to make the expressions equal on both sides of the = sign:

(a) 13 + 4 = __ + 6

(b) 22 + __ = 6 × 5

(d) 34 – __ = 25

Solution:

Question 2: Arrange the following expressions in ascending (increasing) order of their values.

(a) 67 – 19

(b) 67 – 20

(d) 5 × 11

(e) 120 ÷ 3

Solution:

NCERT In-Text Questions (Page 26)

Comparing Expressions

Question: Use ‘>’ or ‘<’ or ‘=’ in each of the following expressions to compare them. Can you do it without complicated calculations? Explain your thinking in each case.

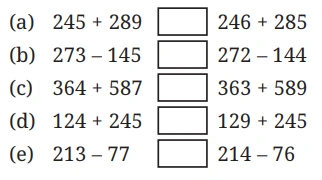
Solution:

NCERT In-Text Questions (Pages 28-29)

Terms in Expressions

Question: Check if replacing subtraction by addition in this way does not change the value of the expression, by taking different examples.

Solution:

Question: Can you explain why subtracting a number is the same as adding its inverse, using the Token Model of integers that we saw in the Class 6 textbook of mathematics?

Solution:

Absolutely—let’s walk through it the Token Model way, just like in the Class 6 textbook

The Token Model (quick reminder)

+1 token (often a white or yellow counter) represents +1
–1 token (often a black or red counter) represents –1
A +1 token and a –1 token together make zero (they cancel each other)

What does “subtracting a number” mean?

To subtract a number, we try to remove its tokens.

But here’s the catch
Sometimes the tokens we want to remove aren’t there!

That’s where the idea of adding the inverse comes in.

Example 1: ( 3 – 2 )

Using tokens

Start with 3 positive tokens:
( + + + )
Subtract 2 → remove 2 positive tokens

Left with:

( + )

So, ( 3 – 2 = 1 ) ✔️

Example 2: ( 3 – 5 )

Step 1: Start with 3

Tokens:
( + + + )

Step 2: Try to subtract 5 positives

Uh-oh 😯 we only have 3 positive tokens, but we need to remove 5.

Step 3: Add zero pairs

Remember:
A (+1, –1) pair = 0, so adding it doesn’t change the number.

Add two zero pairs:

( + + + ; (+ -) ; (+ -) )

Now we have 5 positive tokens.

Step 4: Remove 5 positives

Remove all 5 positive tokens. Left with two minus

( – – )

So,
[3 – 5 = -2]

Now see the magic

Instead of saying subtract 5, notice what actually happened:

We added two –1 tokens
The final result came from adding negative tokens

So,
[3 – 5 = 3 + (-5)]

Why subtracting is the same as adding the inverse

In the Token Model:

Subtracting a number means removing its tokens
If the needed tokens aren’t there, we add zero pairs
Adding zero pairs introduces inverse tokens
After cancellation, what really happens is adding the opposite (inverse)

Key idea to remember 🌟

Subtracting a number is the same as adding its inverse because both actions leave the same tokens after all zero pairs cancel out.

That’s why:
[a – b = a + (-b)]

NCERT In-Text Question (Page 29)

Question: Complete the Table

Let’s complete it step by step, using the idea “every expression can be written as a sum of its terms”.
(Remember: subtraction becomes adding a negative, and multiplication stays inside a term.)

Completed Table

Expression	Expression as the sum of its terms	Terms
13 − 2 + 6	13 + (−2) + 6	13, −2, 6
5 + 6 × 3	5 + (6 × 3)	5, 6 × 3
4 + 15 − 9	4 + 15 + (−9)	4, 15, −9
23 − 2 × 4 + 16	23 + (−2 × 4) + 16	23, −2 × 4, 16
28 + 19 − 8	28 + 19 + (−8)	28, 19, −8

Key idea to remember ⭐

Terms are separated by + or − signs
A minus sign means the term is negative
Multiplication stays within a term

If you want, I can also help you turn this into a rule for identifying terms that students can easily memorise. 😊

Rules to Find the terms from the expression: (Just for Student Knowledge)

Nice Let’s turn it into a clear, Class-6 friendly rule you can remember and use every time.

Rule: How to Identify Terms in an Expression

First rewrite the expression using only “+” signs.
- Change subtraction into adding a negative.
- Example:
  ( a – b = a + (-b) )
Each part separated by a “+” sign is a term.
Multiplication stays inside a term.
- Do not split numbers that are multiplied.

Apply the Rule (quick check)

Example: ( 23 – 2 x 4 + 16 )

Step 1: Change subtraction
[23 + (-2 x 4) + 16]

Step 2: Identify terms

23
−2 × 4
16

✔️ These are the terms.

One-line takeaway 🌟

Terms are the parts of an expression that are added together after changing every subtraction into addition of a negative.

If you want, I can also give a one-minute classroom activity or a fill-in-the-blanks exercise based on this rule.

Question: Does changing the order in which the terms are added give different values?

Solution:

Short answer (in student language):

No. Changing the order of adding terms does not change the value.

Let’s see why.

Using an example

Take this expression:
[13 + (-2) + 6]

Add in the given order:

(13 + (-2) = 11)
(11 + 6 = 17)

Now change the order:
[6 + 13 + (-2)]

(6 + 13 = 19)
(19 + (-2) = 17)

👉 Same answer: 17

Why does this happen?

This works because addition of integers is commutative.

That’s a fancy word, but the idea is simple:

When we add numbers, we can change their order and the sum stays the same.

Symbolically:
[a + b = b + a]

Think using the Token Model 🟡🔴

Each +1 token adds 1
Each –1 token subtracts 1
The final value depends only on how many + tokens and − tokens are there,
not on the order in which you count them.

So whether you add:

all positives first, or
positives and negatives mixed,

the leftover tokens after cancellation are the same.

Important note

This works for addition, but not for subtraction.

Example:

(5 – 3 ≠ 3 – 5)

That’s why we first rewrite subtraction as addition of a negative.

Final takeaway 🌟

Changing the order of terms in addition does not change the value of the expression.

Question: Will this also hold when there are terms having negative numbers as well? Take some more expressions and check.

Solution:

Yes — it still holds even when some (or all) of the terms are negative.

Let’s check it, not just claim it.

Example 1

[(-3) + 7 + (-4)]

Order 1:

((-3) + 7 = 4)
(4 + (-4) = 0)

Order 2 (changed order):

[7 + (-4) + (-3)]

(7 + (-4) = 3)
(3 + (-3) = 0)

✅ Same value: 0

Example 2

[(-5) + (-2) + 9]

Order 1:

((-5) + (-2) = -7)
(-7 + 9 = 2)

Order 2:

[9 + (-5) + (-2)]

(9 + (-5) = 4)
(4 + (-2) = 2)

✅ Same value: 2

Example 3 (all negative terms)

[(-4) + (-6) + (-1)]

Order 1:

((-4) + (-6) = -10)
(-10 + (-1) = -11)

Order 2:

[(-1) + (-4) + (-6)]

((-1) + (-4) = -5)
(-5 + (-6) = -11)

✅ Same value: –11

Think with the Token Model 🟡🔴

Positive numbers → + tokens
Negative numbers → – tokens
When you add, you’re just putting tokens together
Cancellation happens no matter the order

So the final number depends only on:

how many + tokens
how many − tokens

not on the order they are counted.

Big conclusion 🌟

Changing the order of addition does not change the sum, even when negative numbers are involved.

This property is called the commutative property of addition, and it works for all integers.

If you want, we can now check what happens when we change the grouping instead of the order—that leads to another important property 👀

NCERT In-Text Question Page 30

Question: Can you explain why this is happening using the Token Model of integers that we saw in the Class 6 textbook of mathematics?

Solution:

Yes—let’s explain why this happens using the Token Model, exactly the way Class 6 introduces integers

Token Model reminder

+1 token represents +1
−1 token represents −1
One +1 token and one −1 token make zero (they cancel)

What does “adding integers” mean in the Token Model?

When we add integers, we put together all their tokens in one place.

The final value depends only on how many + tokens and − tokens remain after cancellation.

Example 1: ( (-3) + 7 + (-4) )

Step 1: Show tokens

−3 → 🔴🔴🔴
+7 → 🟡🟡🟡🟡🟡🟡🟡
−4 → 🔴🔴🔴🔴

Step 2: Put all tokens together

Total tokens:

🟡 × 7
🔴 × 7

Step 3: Cancel zero pairs

Each 🟡 cancels with one 🔴.

All tokens cancel → 0 remains

Now change the order

[7 + (-4) + (-3)]

Token view

You still have 7 positive tokens
You still have 7 negative tokens

Same cancellations → 0 remains

🔑 Nothing changes, because:

The number of tokens did not change
Only the order of counting changed

Example 2: ( (-5) + (-2) + 9 )

Tokens:

🔴 × 7
🟡 × 9

After cancellation:

2 🟡 left → +2

Change the order:
[9 + (-5) + (-2)]

You still get:

🔴 × 7
🟡 × 9

Same cancellation → +2

Why order never matters in addition (Token explanation)

Addition means collecting tokens
Cancellation depends only on matching pairs
Tokens do not remember the order they were added in

So:

As long as the same tokens are present, the final result is the same—no matter the order.

Big idea (Class 6 language)

In addition of integers, changing the order of the numbers does not change the sum because the number of positive and negative tokens remains the same.

That’s why the addition of integers is commutative.

If you want, we can now connect this to changing the grouping of terms (brackets) using tokens as well.

Question: Will this also hold when there are terms having negative numbers as well? Take some more expressions and check.

Solution:

Yes — it still holds even when the terms themselves are negative.

Let’s check carefully using the Token Model, with a few different kinds of expressions.

Example 1

[(-6) + 4 + (-2)]

Tokens

−6 → 🔴🔴🔴🔴🔴🔴
+4 → 🟡🟡🟡🟡
−2 → 🔴🔴

Total:

🔴 × 8
🟡 × 4

After cancellation:

4 🔴 left → −4

Change the order

[4 + (-2) + (-6)]

Tokens are exactly the same:

🔴 × 8
🟡 × 4

After cancellation → −4

✔️ Same value

Example 2

[(-3) + (-5) + 10]

Tokens

🔴 × 8
🟡 × 10

After cancellation:

2 🟡 left → +2

Change the order

[10 + (-5) + (-3)]

Still:

🔴 × 8
🟡 × 10

After cancellation → +2

✔️ Same value

Example 3 (all negative terms)

[(-2) + (-7) + (-4)]

Tokens

🔴 × 13

No cancellation possible.

Result → −13

Change the order

[(-7) + (-4) + (-2)]

Tokens unchanged → −13

✔️ Same value

Why this always works (Token explanation)

Every number contributes a fixed number of tokens
Changing the order only changes when tokens are added, not how many
Cancellation depends only on matching + and − tokens

So:

Even when terms are negative, changing the order of addition does not change the final value.

Final takeaway 🌟 (Class 6 level)

The sum of integers depends on the number of positive and negative tokens, not on the order in which they are added.

That’s why the commutative property of addition works for all integers, positive or negative.

Question: Can you explain why this is happening using the Token Model of integers that we saw in the Class 6 textbook of mathematics?

Solution:

Yes—let’s explain why this happens using the Token Model, just the way it is meant in the Class 6 textbook 😊

Token Model: the basic idea

+1 token stands for +1
–1 token stands for –1
One +1 token and one –1 token together make 0 (they cancel each other)

What does addition mean in the Token Model?

When we add integers, we are simply putting together all the tokens from each term.

👉 The value of the expression depends only on how many + tokens and − tokens are present in total, not on the order in which they are added.

Why order does not matter (key reason)

Changing the order of addition:

does not change the number of + tokens
does not change the number of − tokens

Since cancellation happens only between pairs of opposite tokens, the leftover tokens are always the same.

See it with an example

Take:
[(-6) + 4 + (-2)]

Tokens added:

−6 → 6 negative tokens
+4 → 4 positive tokens
−2 → 2 negative tokens

Total:

8 negative tokens
4 positive tokens

After cancelling 4 pairs:

4 negative tokens remain → −4

Now change the order:
[4 + (-2) + (-6)]

The tokens are exactly the same:

8 negative tokens
4 positive tokens

Same cancellations → −4

Why this works even with negative terms

A negative number just means more negative tokens
Adding them earlier or later does not affect cancellation
Tokens do not “remember” the order in which they were added

Big idea (Class 6 language)

In addition of integers, the sum depends on the total number of positive and negative tokens. Since this does not change with order, the value of the sum remains the same.

That’s why changing the order of terms in addition does not change the value, even when negative numbers are involved.

NCERT In-Text Question Page 31

Question: Does adding the terms of an expression in any order give the same value? Take some more expressions and check. Consider expressions with more than 3 terms also.

Solution:

Yes 👍 adding the terms of an expression in any order always gives the same value, even when

there are negative numbers, and
there are more than three terms.

Let’s check with several expressions.

Example 1 (4 terms, mix of + and −)

[5 + (-3) + 7 + (-4)]

Order 1:

(5 + (-3) = 2)
(2 + 7 = 9)
(9 + (-4) = 5)

Change the order:

[7 + 5 + (-4) + (-3)]

(7 + 5 = 12)
(12 + (-4) = 8)
(8 + (-3) = 5)

✅ Same value: 5

Example 2 (5 terms)

[(-2) + 6 + (-5) + 3 + (-2)]

Order 1:

((-2) + 6 = 4)
(4 + (-5) = -1)
(-1 + 3 = 2)
(2 + (-2) = 0)

Change the order:

[6 + 3 + (-2) + (-5) + (-2)]

(6 + 3 = 9)
(9 + (-2) = 7)
(7 + (-5) = 2)
(2 + (-2) = 0)

✅ Same value: 0

Example 3 (6 terms, more negatives)

[(-4) + 8 + (-3) + (-1) + 2 + (-2)]

Order 1:

((-4) + 8 = 4)
(4 + (-3) = 1)
(1 + (-1) = 0)
(0 + 2 = 2)
(2 + (-2) = 0)

Change the order:

[8 + 2 + (-4) + (-3) + (-1) + (-2)]

(8 + 2 = 10)
(10 + (-4) = 6)
(6 + (-3) = 3)
(3 + (-1) = 2)
(2 + (-2) = 0)

✅ Same value: 0

Why this always works (Token Model idea)

Each term contributes a fixed number of + tokens or − tokens
Changing the order does not change the total number of tokens
Cancellation of opposite tokens happens no matter the order

So the final result depends only on:

how many + tokens there are
how many − tokens there are

Final conclusion (Class 6 level)

Yes, adding the terms of an expression in any order gives the same value, even for expressions with many terms and negative numbers.

This is because addition of integers is commutative, and the Token Model clearly shows why.

Question: Can you explain why this is happening using the Token Model of integers that we saw in the Class 6 textbook of mathematics?

Solution:

Yes—let’s explain why this happens using the Token Model, exactly in the spirit of the Class 6 textbook 😊

1. Token Model recap

+1 token represents +1
–1 token represents –1
A (+1, –1) pair makes 0 and can be removed

2. What does adding many terms mean?

When an expression has many terms, adding them means:

Put together all the tokens from every term into one collection.

Each term contributes:

positive tokens if it is positive
negative tokens if it is negative

3. Why order does not matter

Suppose an expression has:

P positive tokens
N negative tokens

No matter which term you add first:

the total number of + tokens is still P
the total number of − tokens is still N

Cancellation depends only on how many opposite pairs can be formed, not on the order of adding.

4. See it with a 5-term example

[5 + (-3) + 7 + (-4) + (-2)]

Tokens contributed

+5 → 🟡×5
−3 → 🔴×3
+7 → 🟡×7
−4 → 🔴×4
−2 → 🔴×2

Total:

🟡×12
🔴×9

Cancel 9 pairs → 🟡×3 remain
Result = +3

Change the order

[(-4) + 7 + (-2) + 5 + (-3)]

Tokens are still:

🟡×12
🔴×9

Same cancellations → +3

5. Core reason (Token explanation)

Tokens do not change their value
Tokens do not depend on order
Cancellation happens whenever a + and − meet

So:

As long as the same tokens are present, the final value must be the same.

6. Big idea (Class 6 takeaway 🌟)

Changing the order of addition does not change the sum because the total number of positive and negative tokens remains unchanged.

That’s why adding the terms of an expression in any order always gives the same value, even with many terms and negative numbers.

Question: Manasa is adding a long list of numbers. It took her five minutes to add them all and she got the answer 11749. Then she realised that she had forgotten to include the fourth number 9055. Does she have to start all over again? (Numbers list: 1342, 774, 8611, 9055, 1022)

Solution:

No — she does not have to start all over again.

Let’s see why, using the idea we’ve been discussing about addition.

What Manasa has already done

She added all the numbers except the fourth one and got:
[11749]

The missing number is:
[9055]

Key idea (very important!)

When we add numbers:

the order does not matter
we can add a missed number later

So forgetting a number just means it was not included yet.

What should Manasa do now?

She simply needs to add the forgotten number to her answer:

[11749 + 9055]

Let’s add:

(11749 + 9000 = 20749)
(20749 + 55 = 20804)

Final answer

👉 The correct total is 20,804

Why this works (Token Model thinking 🌟)

Each number adds its own set of tokens
Manasa already counted the tokens for the other numbers
She only missed the tokens for 9055
Adding them at the end gives the same result as adding them earlier

Conclusion

Manasa does not need to start again. She can just add the missed number to her previous sum.

That’s the power of addition being order-independent .

Question: Manasa is going outside to play. Her mother says, “Wear your hat and shoes!” Which one should she wear first?

Solution:

Nice real-life question 😊

It doesn’t matter which one Manasa wears first.
She can wear the hat first and then the shoes, or the shoes first and then the hat—the result is the same: she is ready to go out.

Why this makes sense

Wearing a hat and wearing shoes are two independent actions.
Doing one does not affect the other.
Changing the order doesn’t change the final outcome.

Link to maths (Class 6 idea 🌟)

This is just like adding numbers:

You can add them in any order
The final sum remains the same

Just as:
[a + b = b + a]

Simple takeaway

When actions don’t depend on each other, the order doesn’t matter.

So Manasa can choose whichever she likes first—and still head out to play 😄

NCERT In-Text Question Page 32

Question: If the total number of friends goes up to 7 and the tip remains the same, how much will they have to pay? Each dosa cost ₹23, and they wish to thank the waiter by
tipping ₹5. Write an expression for this situation and identify its terms.

Solution:

Got it 👍 Let’s do this neatly, step by step.

Given

Cost of one dosa = ₹23
Number of friends = 7 (so 7 dosas)
Tip = ₹5 (same tip, not per person)

Writing the expression

Cost of 7 dosas:
[7 x 23]

Add the tip:
[7 x 23 + 5]

👉 Expression:
[7 x 23 + 5]

Finding the total amount

[7 \times 23 = 161]

[161 + 5 = 166]

👉 Total amount to be paid = ₹166

Identifying the terms

First rewrite the expression as a sum:
[(7 x 23) + 5]

Terms are:

(7 x 23)
(5)

Final answer 🌟

Expression: (7 x 23 + 5)
Terms: (7 x times 23,; 5)
Total amount: ₹166

Question: Children in a class are playing “Fire in the mountain, run, run, run!”. Whenever the teacher calls out a number, students are supposed to arrange themselves in groups of that number. Whoever is not part of the announced group size, is out. Ruby wanted
to rest and sat on one side. The other 33 students were playing the game in the class. The teacher called out ‘5’. Once children settled, Ruby wrote 6 × 5 + 3 Think and discuss why she wrote this. The expression written as a sum of terms is—

Solution:

Let’s think it through calmly, just like Ruby did

What is happening in the game?

33 students are playing.
The teacher calls out 5.
Students must form groups of 5.
Anyone left out is out.

How many full groups of 5 can be formed?

From 33 students:

(33 ÷ 5 = 6) groups, with 3 students left over.

So we have:

6 complete groups of 5 students
3 students not in any group (out)

Why did Ruby write (6 × 5 + 3)?

Because:

(6 × 5) represents the students who formed complete groups
(+ 3) represents the students left out

And:
[6 × 5 + 3 = 30 + 3 = 33]

So Ruby used the expression to show how all 33 students are accounted for.

Expression written as a sum of terms

[(6 × 5) + 3]

The terms are:

(6 × 5)
(3)

Big idea 🌟

Any number can be written as
(number of full groups × group size) + number left over.

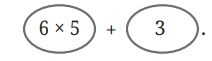
That’s exactly what Ruby noticed—and neatly captured with her expression.

NCERT In-Text Question Page 33

Question: For each of the cases below, write the expression and identify its terms:

If the teacher had called out ‘4’, Ruby would write __

If the teacher had called out ‘7’, Ruby would write __

Write expressions like the above for your class size.

Solution:

Let’s do this step by step, just like Ruby would reason it out 😊

We know:

Number of students playing = 33
Ruby always writes:
[(number of full groups) x (group size)] + (students left out)

1️⃣ If the teacher had called out 4

Divide 33 by 4:

(33 ÷ 4 = 8) groups, 1 student left

Expression:

[8 × 4 + 1]

Written as a sum of terms:

[(8 × 4) + 1]

Terms:

(8 × 4)
(1)

2️⃣ If the teacher had called out 7

Divide 33 by 7:

(33 ÷ 7 = 4) groups, 5 students left

Expression:

[4 × 7 + 5]

Written as a sum of terms:

[(4 × 7) + 5]

Terms:

(4 × 7)
(5)

3️⃣ For your class size (general form)

Let:

total number of students = (N)
number called out by the teacher = (k)

Then Ruby would write:
[q × k + r]
where:

(q) = number of complete groups
(r) = number of students left out ((0 \le r < k))

Expression as a sum of terms:

[(q × k) + r]

Terms:

(q × k)
(r)

Big idea 🌟

Any number can be written as
(groups × group size) + remainder.

That’s exactly the pattern Ruby spotted in the game!

Question: Identify the terms in the two expressions above.

Solution:

Question: Can you think of some more ways of giving ₹432 to someone?

Solution:

Let’s identify them clearly 😊

The two expressions we wrote were:

(8 × 4 + 1)
(4 × 7 + 5)

Expression 1: (8 × 4 + 1)

First write it as a sum:
[(8 × 4) + 1]

Terms

(8 × 4)
(1)

Expression 2: (4 × 7 + 5)

Write it as a sum:
[(4 × 7) + 5]

Terms

(4 × 7)
(5)

Key reminder 🌟

Terms are the parts of an expression that are added together. Multiplication stays inside a term.

So in both cases, there are two terms:

one multiplication term (groups formed)
one number showing students left out.

NCERT In-Text Question Page 34

Figure it Out

Question 1: Find the values of the following expressions by writing the terms in each case.

(a) 28 – 7 + 8
(b) 39 – 2 × 6 + 11
(c) 40 – 10 + 10 + 10
(d) 48 – 10 × 2 + 16 ÷ 2
(e) 6 × 3 – 4 × 8 × 5

Solution:

Let’s do each one systematically, exactly as taught: first write the expression as a sum of its terms, then find the value.

(a) (28 – 7 + 8)

Write as a sum of terms

[28 + (-7) + 8]

Terms

28
−7
8

Value

[28 – 7 + 8 = 21 + 8 = \boxed{29}]

(b) (39 – 2 × 6 + 11)

Write as a sum of terms

(Remember: multiplication stays inside a term)
[39 + (-2 × 6) + 11]

Terms

39
−2 × 6
11

Value

[2 × 6 = 12]
[39 – 12 + 11 = 27 + 11 = \boxed{38}]

(c) (40 – 10 + 10 + 10)

Write as a sum of terms

[40 + (-10) + 10 + 10]

Terms

40
−10
10
10

Value

[40 – 10 = 30, 30 + 10 + 10 = 40]

(d) (48 – 10 × 2 + 16 ÷ 2)

Write as a sum of terms

[48 + (-10 × 2) + (16 ÷ 2)]

Terms

48
−10 × 2
16 ÷ 2

Value

[10 × 2 = 20, 16 ÷ 2 = 8]
[48 – 20 + 8 = 28 + 8 = 36]

(e) (6 × 3 – 4 × 8 × 5)

Write as a sum of terms

[(6 × 3) + (-4 × 8 × 5)]

Terms

6 × 3
−4 × 8 × 5

Value

[6 × 3 = 18]
[4 × 8 × 5 = 160]
[18 – 160 = \boxed{-142}]

Final answers

(a) 29
(b) 38
(c) 40
(d) 36
(e) −142

If you want, we can now connect this to why order of adding terms doesn’t matter using the Token Model again 😊

Question 2: Write a story/situation for each of the following expressions and find their values.

(a) 89 + 21 – 10
(b) 5 × 12 – 6
(c) 4 × 9 + 2 × 6

Solution:

Nice question—this is exactly how maths connects to real life. Let’s write a simple story for each expression and then find its value.

(a) (89 + 21 – 10)

Story

A library had 89 books on a shelf.
The librarian added 21 new books, but later 10 books were issued to students.
How many books are left on the shelf?

Value

[89 + 21 = 110]
[110 – 10 = \boxed{100}]

(b) (5 × 12 – 6)

Story

A shopkeeper packed 5 boxes, each containing 12 chocolates.
On the way, 6 chocolates were damaged and could not be sold.
How many chocolates are left?

Value

[5 × 12 = 60]
[60 – 6 = \boxed{54}]

(c) (4 × 9 + 2 × 6)

Story

There are 4 packets of pencils, with 9 pencils in each packet, and 2 more packets, with 6 pencils in each.

How many pencils are there altogether?

Value

[4 × 9 = 36]
[2 × 6 = 12]
[36 + 12 = \boxed{48}]

Final answers 🌟

(a) 100
(b) 54
(c) 48

Question 3: For each of the following situations, write the expression describing the situation, identify its terms and find the value of the expression.

(a) Queen Alia gave 100 gold coins to Princess Elsa and 100 gold coins to Princess Anna last year. Princess Elsa used the coins to start a business and doubled her coins. Princess Anna bought jewellery and has only half of the coins left. Write an expression describing how many gold coins Princess Elsa and Princess Anna together have.

Solution:-

Let’s translate the story into maths step by step.

Queen Alia gave 100 coins to each princess.

Princess Elsa
She doubled her coins:
[2 x 100]

Princess Anna
She has half of her coins left:
[100 ÷ 2]

Expression for their total coins together

[(2 x 100) + (100 ÷ 2)]

Finding the value

[2 x 100 = 200]
[100 ÷ 2 = 50]

[200 + 50 = 25}]

Final answer 🌟

Expression: [(2 x 100) + (100 ÷ 2)]
Total number of gold coins together: 250

(b) A metro train ticket between two stations is ₹40 for an adult and ₹20 for a child. What is the total cost of tickets?

(i) for four adults and three children?

(ii) for two groups having three adults each?

Solution:-

Let’s turn the situation into expressions first, then find the total cost 😊

Given

Cost of one adult ticket = ₹40
Cost of one child ticket = ₹20

(i) Four adults and three children

Expression

Cost for 4 adults = (4 × 40)
Cost for 3 children = (3 × 20)

Total cost:
[(4 × 40) + (3 × 20)]

Value

[4 × 40 = 160]
[3 × 20 = 60]

[160 + 60 = ₹220]

(ii) Two groups having three adults each

First find the total number of adults:

(2 × 3 = 6) adults

Expression

[6 × 40]

Value

[6 × 40 = ₹240]

Final answers

(i) Total cost = ₹220
(ii) Total cost = ₹240

(c) Find the total height of the window by writing an expression describing the relationship among the measurements shown in the picture.

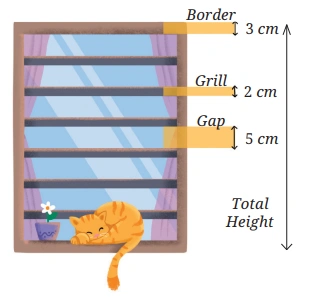
Solution:

Let’s carefully read the picture and translate it into maths 😊

What we see in the picture

Border at the top = 3 cm
Each grill = 2 cm
Each gap between grills = 5 cm

From the picture, there are:

6 grills
7 gaps (gaps are always one less than the number of grills)
2 Border Up and Below

Writing the expression

Total height = (height of border x 2) + (height of all grills) + (height of all gaps)

[= (3 x 2) + (2 × 6) + (5 × 7)]

Finding the value

[3 × 2 = 6]
[2 × 6 = 12]
[5 × 7 = 35]

[6 + 12 + 35 = 53]

Final answer 🌟

Expression: (3 x 2) + (2 × 6) + (5 × 7)
Total height of the window: 53 cm

This neatly shows how the total height is built from border + grills + gaps 👍

NCERT In-Text Question Page 34

Question:

Solution:-

Figure it Out

Question 1: Fill in the blanks with numbers, and boxes with operation signs such that the expressions on both sides are equal.

(a) 24 + (6 – 4) = 24 + 6 _

(b) 38 + (_ _) = 38 + 9 – 4

(d) 24 – 6 – 4 = 24 – 6 _

(e) 27 – (8 + 3) = 27 8 3

(f) 27– (_ _) = 27 – 8 + 3

Solution:

(a) 24 + (6 – 4) = 24 + 6 – 4

(b) 38 + (9 – 4) = 38 + 9 – 4

(d) 24 – 6 – 4 = 24 – 6 + (-4)

(e) 27 – (8 + 3) = 27 – 8 – 3

(f) 27 – (8 – 3) = 27 – 8 + 3

Question 2: Remove the brackets and write the expression having the same value.

(a) 14 + (12 + 10)
(b) 14 – (12 + 10)
(c) 14 + (12 – 10)
(d) 14 – (12 – 10)
(e) –14 + 12 – 10
(f) 14 – (–12 – 10)

Solution:

(a) 14 + (12 + 10) = 14 + 12 + 10

(b) 14 – (12 + 10) = 14 – 12 – 10

(d) 14 – (12 – 10) = 14 – 12 + 10

(e) -14 + 12 – 10 = -14 + 12 – 10

(f) 14 – (-12 – 10) = 14 + 12 + 10

Question 3: Find the values of the following expressions. For each pair, first try to guess whether they have the same value. When are the two expressions equal?

(a) (6 + 10) – 2 and 6 + (10 – 2)

(b) 16 – (8 – 3) and (16 – 8) – 3

Solution:

(a)

Guess: They look similar, so maybe they’re equal.

[(6 + 10) – 2 = 16 – 2 = 14]

[6 + (10 – 2) = 6 + 8 = 14]

✅ Same value: 14

(b)

Guess: Brackets are in different places, so they might be different.

[16 – (8 – 3) = 16 – 5 = 11]

[(16 – 8) – 3 = 8 – 3 = 5]

❌ Not equal
Values: 11 and 5

(c)

Guess: Second expression rewrites subtraction using negative numbers, so they may be equal.

[27 – (18 + 4) = 27 – 22 = 5]

[27 + (-18 – 4) = 27 + (-22) = 5]

✅ Same value: 5

🧠 When are two such expressions equal?

Two expressions are equal when:

Brackets are rearranged without changing signs, or
A subtraction is rewritten as adding a negative number, keeping the total effect the same.

📌 Key idea to remember

Addition is associative → brackets don’t change the result.
Subtraction is not associative → brackets do matter.

NCERT In-Text Page 38

Question 4: In each of the sets of expressions below, identify those that have the same value. Do not evaluate them, but rather use your understanding of terms.

(a) 319 + 537, 319 – 537, – 537 + 319, 537 – 319

(b) 87 + 46 – 109, 87 + 46 – 109, 87 + 46 – 109, 87 – 46 + 109, 87 – (46 + 109), (87 – 46) + 109

Solution:

Good one — this is all about seeing expressions as collections of terms, not calculating numbers. Let’s do it cleanly.

(a)

Expressions given:

(319 + 537)
(319 – 537)
(-537 + 319)
(537 – 319)

Look at the terms

(319 + 537) has +319 and +537
(-537 + 319) has +319 and −537
(319 – 537) has +319 and −537
(537 – 319) has +537 and −319

Same-value groups

(319 – 537) and (-537 + 319)
👉 same terms, just reordered

✅ Answer (a):
[319 – 537 = -537 + 319]

(b)

(b) 87 + 46 – 109, 87 + 46 – 109, 87 + 46 – 109, 87 – 46 + 109, 87 – (46 + 109), (87 – 46) + 109

Exactly same →

87 + 46 – 109, 87 + 46 – 109, 87 + 46 – 109.

Same value →

87 – 46 + 109 and (87 – 46) + 109, 87 – (46 + 109) → Follow the associative property of addition.

🔑 Big idea to remember

Two expressions have the same value if they contain exactly the same terms with the same signs, no matter the order or brackets (as long as signs don’t change).

Question 5: Add brackets at appropriate places in the expressions such that they lead to the values indicated.

(a) 34 – 9 + 12 = 13

(b) 56 – 14 – 8 = 34

Solution:

Let’s do this by forcing the operations to happen in the right order using brackets, not by changing numbers.

(a)

Expression:
(34 – 9 + 12)
Target value: 13

If we first add (9 + 12):

[34 – (9 + 12)] = 34 – 21 = 13]

✅ Answer:
[34 – (9 + 12)]

(b)

Expression:
(56 – 14 – 8)
Target value: 34

If we subtract (14 – 8) first:

[{56 – (14 – 8)} = 56 – 6 = 50 not correct})]

Instead, group the first two subtractions together:

[{(56 – 14) – 8} = 42 – 8 = 34]

✅ Answer:
[(56 – 14) – 8]

(c)

Expression:
(-22 – 12 + 10 + 22)
Target value: −22

Group the middle terms so they cancel out:

[{-22 – (12 – 10 + 22)}]

Inside the bracket:
(12 – 10 + 22 = 24)

So:
[-22 – 24 = -22 ❌]

Try grouping so (+22) cancels (−22):

[boxed{(-22 – 12 + 10) + 22}]

Inside:
[-22 – 12 + 10 = -24]

Then:
[-24 + 22 = -22]

✅ Answer:
[(-22 – 12 + 10) + 22]

(a) (34 – (9 + 12))
(b) ((56 – 14) – 8)
(c) ((-22 – 12 + 10) + 22)

Question 6: Using only reasoning of how terms change their values, fill the blanks to make the expressions on either side of the equality (=) equal.

(a) 423 + _____ = 419 + _____

(b) 207 – 68 = 210 – _____

Solution:

Let’s balance both sides by thinking about how terms change, not by calculating fully.

(a) 423 + _ = 419 + _

Notice:

423 is 4 more than 419

To keep the totals equal, the number added to 423 must be 4 less than the number added to 419.

So we can write:
[423 + 5] = [419 + 9]

(b) 207 – 68 = 210 – _____

Notice:

210 is 3 more than 207

To keep the result the same, we must subtract 3 more on the right side.

So: [207 – 68 = 210 – 71]

✅ Final answers

(a) (423 + 5 = 419 + 9)
(b) (207 – 68 = 210 – 71)

💡 Key idea:
If one number increases, the other must change by the same amount in the opposite way to keep equality.

Question 7: Using the numbers 2, 3 and 5, and the operators ‘+’ and ‘–’, and brackets, as necessary, generate expressions to give as many different values as possible. For example, 2 – 3 + 5 = 4 and 3 – (5 – 2) = 0.

Solution:

Let’s systematically explore all possible values we can generate using 2, 3, 5 with the operators + and –, and brackets where needed.

Step 1: Start with simple linear combinations

Without brackets, just permutations of addition and subtraction:

(2 + 3 + 5 = 10)
(2 + 3 – 5 = 0)
(2 – 3 + 5 = 4)
(2 – 3 – 5 = -6)
(3 + 2 + 5 = 10) (same as above)
(3 + 2 – 5 = 0)
(3 – 2 + 5 = 6)
(3 – 2 – 5 = -4)
(5 + 2 + 3 = 10)
(5 + 2 – 3 = 4)
(5 – 2 + 3 = 6)
(5 – 2 – 3 = 0)

So far, values: 10, 0, 4, -6, 6, -4

Step 2: Use brackets to change grouping

Brackets can alter subtraction outcomes:

((2 + 3) – 5 = 0)
(2 + (3 – 5) = 0)
((2 – 3) + 5 = 4)
(2 – (3 + 5) = -6)
((3 + 5) – 2 = 6)
(3 + (5 – 2) = 6)
((3 – 5) + 2 = 0)
(3 – (5 + 2) = -4)
((5 + 2) – 3 = 4)
(5 + (2 – 3) = 4)
((5 – 2) + 3 = 6)
(5 – (2 + 3) = 0)

These don’t add new values beyond what we already found.

Step 3: Collect unique results

From all permutations and bracketings, the distinct values we can generate are:

[ {-6, -4, 0, 4, 6, 10} ]

✅ Final Answer:
Using 2, 3, 5 with +, –, and brackets, the possible values are:
-6, -4, 0, 4, 6, 10

Question 8: Whenever Jasoda has to subtract 9 from a number, she subtracts 10 and adds 1 to it. For example, 36 – 9 = 26 + 1.

(a) Do you think she always gets the correct answer? Why?

(b) Can you think of other similar strategies? Give some examples.

Solution:

Perfect, let’s break this down step by step in a clear, CBSE‑style explanation 👇

(a) Does Jasoda always get the correct answer? Why?

Yes, Jasoda always gets the correct answer.
Here’s why:

Subtracting 9 is the same as subtracting 10 and then adding 1 back.
Mathematically:
[ n – 9 = (n – 10) + 1 ]
Example:
[ 36 – 9 = (36 – 10) + 1 = 26 + 1 = 27 ]
This works for any number (n), because the difference between subtracting 9 and subtracting 10 is exactly 1.

So her method is a clever shortcut that always gives the right result.

(b) Other similar strategies

Yes, we can create similar strategies for subtraction (and even addition).

Examples:

Subtracting 8
[ n – 8 = (n – 10) + 2 ]
Example: (54 – 8 = (54 – 10) + 2 = 44 + 2 = 46)
Subtracting 19
[ n – 19 = (n – 20) + 1 ]
Example: (83 – 19 = (83 – 20) + 1 = 63 + 1 = 64)
Subtracting 99
[ n – 99 = (n – 100) + 1 ]
Example: (250 – 99 = (250 – 100) + 1 = 150 + 1 = 151)
Adding 9
[ n + 9 = (n + 10) – 1 ]
Example: (47 + 9 = (47 + 10) – 1 = 57 – 1 = 56)
Adding 19
[ n + 19 = (n + 20) – 1 ]

✅ Final Answer (student‑friendly):
(a) Yes, Jasoda always gets the correct answer because subtracting 9 is the same as subtracting 10 and then adding 1.
(b) Similar strategies:

Subtract 8 → subtract 10 and add 2
Subtract 19 → subtract 20 and add 1
Subtract 99 → subtract 100 and add 1
Add 9 → add 10 and subtract 1

Question 9: Consider the two expressions: a) 73 – 14 + 1, b) 73 – 14 – 1. For each of these expressions, identify the expressions from the following collection that are equal to it.

(a) 73 – (14 + 1)

b) 73 – (14 – 1)

d) 73 + (– 14 – 1)

Solution:

Alright, let’s carefully solve this step by step in a clear, exam‑style format 👇

Given Expressions:

Expression A: (73 – 14 + 1)
Expression B: (73 – 14 – 1)

We need to compare each with the collection:

(a) (73 – (14 + 1))
(b) (73 – (14 – 1))
(c) (73 + (-14 + 1))
(d) (73 + (-14 – 1))

Step 1: Simplify Expression A

[ 73 – 14 + 1 = 59 + 1 = 60 ]

Now check which match:

(a) (73 – (14 + 1) = 73 – 15 = 58) → Not equal
(b) (73 – (14 – 1) = 73 – 13 = 60) → Equal
(c) (73 + (-14 + 1) = 73 + (-13) = 60) → Equal
(d) (73 + (-14 – 1) = 73 + (-15) = 58) → Not equal

✅ So, Expression A (73 – 14 + 1) equals (b) and (c).

Step 2: Simplify Expression B

[ 73 – 14 – 1 = 59 – 1 = 58 ]

Now check which match:

(a) (73 – (14 + 1) = 73 – 15 = 58) → Equal
(b) (73 – (14 – 1) = 73 – 13 = 60) → Not equal
(c) (73 + (-14 + 1) = 73 + (-13) = 60) → Not equal
(d) (73 + (-14 – 1) = 73 + (-15) = 58) → Equal

✅ So, Expression B (73 – 14 – 1) equals (a) and (d).

✨ Final Answer:

(73 – 14 + 1) is equal to (b) and (c)
(73 – 14 – 1) is equal to (a) and (d)

Question: Lhamo and Norbu went to a hotel. Each of them ordered a vegetable cutlet and a rasgulla. A vegetable cutlet costs ₹43 and a rasgulla costs ₹24. Write an expression for the amount they will have to pay.

Solution:-

Let’s solve this step by step in a clear, exam‑style format 👇

Step 1: Cost of one person’s order

Vegetable cutlet = ₹43
Rasgulla = ₹24
[ {Total for one person} = 43 + 24 = 67 ]

Step 2: Cost for two people (Lhamo and Norbu)

Each pays ₹67, so together:
[ {Total amount} = 2 x (43 + 24) ]

Step 3: Simplify the expression

[ 2 x (43 + 24) = 2 x 67 = 134 ]

✅ Final Answer:
The expression for the amount they will have to pay is:
[ 2 x (43 + 24) ]
and the total cost is ₹134.

Page 39

Question: If another friend, Sangmu, joins them and orders the same items, what will be the expression for the total amount to be paid?

Solution:

Great extension of the problem

Step 1: Cost for one person

Vegetable cutlet = ₹43
Rasgulla = ₹24
[ {Total for one person} = 43 + 24 = 67 ]

Step 2: Cost for three people (Lhamo, Norbu, and Sangmu)

Each pays ₹67, so together:
[ {Total amount} = 3 x (43 + 24) ]

Step 3: Simplify the expression

[ 3 x (43 + 24) = 3 x 67 = 201 ]

✅ Final Answer:
The expression for the total amount is:
[ 3 x (43 + 24) ]
and the total cost is ₹201.

Page 40

Question:

5 × 4 + 3 ≠ 5 × (4 + 3). Can you explain why?

Solution:

Excellent question! This is a classic case of understanding the order of operations (BODMAS/PEMDAS) and the role of brackets. Let’s break it down step by step 👇

Expression 1: (5 x 4 + 3)

According to BODMAS, multiplication comes before addition.
So first calculate (5 x 4 = 20).
Then add 3: (20 + 3 = 23).

[ 5 x 4 + 3 = 23 ]

Expression 2: (5 x (4 + 3))

Brackets must be solved first.
Inside the bracket: (4 + 3 = 7).
Then multiply: (5 x 7 = 35).

[ 5 x (4 + 3) = 35 ]

Why are they different?

In (5 x 4 + 3), the multiplication happens first, then addition.
In (5 x (4 + 3)), the bracket forces the addition to happen first, changing the result.
Brackets change the grouping of numbers and therefore change the outcome.

✅ Final Explanation (student‑friendly):
The two expressions are not equal because brackets change the order of operations. Without brackets, multiplication is done first; with brackets, addition inside is done first. That’s why:
[ 5 x 4 + 3 = 23 but 5 x (4 + 3) = 35 ]

Question:

Is 5 × (4 + 3) = 5 × (3 + 4) = (3 + 4) × 5?

Solution:

Great observation! Let’s carefully unpack this 👇

Step 1: Evaluate each expression

(5 x (4 + 3))
Inside the bracket: (4 + 3 = 7).
So, (5 x 7 = 35).
(5 x (3 + 4))
Inside the bracket: (3 + 4 = 7).
So, (5 x 7 = 35).
((3 + 4) x 5)
Inside the bracket: (3 + 4 = 7).
So, (7 x 5 = 35).

Step 2: Compare results

All three expressions give the same result:
[ 35 ]

Step 3: Why are they equal?

Commutative property of addition: (4 + 3 = 3 + 4).
Commutative property of multiplication: (5 x 7 = 7 x 5).
Associative property of grouping: Brackets just ensure addition happens first, but since addition is commutative, the order doesn’t matter.

✅ Final Explanation (student‑friendly):
Yes,
[ 5 x (4 + 3) = 5 x (3 + 4) = (3 + 4) x 5 ]
because addition and multiplication follow the commutative and associative properties.

Page 41

Question: 97 × 25 = 100 × 25 – 3 × 25 Find this value.

Solution:

Let’s solve this step by step.

Step 1: Write the given expression

[ 97 x 25 = 100 x 25 – 3 x 25 ]

Step 2: Simplify each term

(100 x 25 = 2500)
(3 x 25 = 75)

So,
[ 97 x 25 = 2500 – 75 ]

Step 3: Subtract

[ 2500 – 75 = 2425 ]

✅ Final Answer:
[ 97 x 25 = 2425 ]

This is a neat mental math trick: instead of multiplying directly, you adjust to a nearby “easy” number (like 100) and then subtract the extra part.

Question: Use this method to find the following products:

(a) 95 × 8
(b) 104 × 15
(c) 49 × 50

Is this quicker than the multiplication procedure you use generally?

Solution:

Perfect, let’s apply the “nearby easy number” method (like we used for (97 \times 25)) step by step 👇

(a) (95 x 8)

Think of 95 as (100 – 5).

[95 x 8 = (100 – 5) x 8]
[ 95 x 8 = (100 x 8) – (5 x 8) ]
[ 95 x 8 = 800 – 40 = 760 ]

(b) (104 x 15)

Think of 104 as (100 + 4).

[104 x 15 = (11 + 4) x 15]
[ 104 x 15 = (100 x 15) + (4 x 15) ]
[ 104 x 15 = 1500 + 60 = 1560 ]

(c) (49 x 50)

Think of 49 as (50 – 1).

[(49 x 50) = (50 – 1) x 50]
[(49 x 50) = (50 x 50) – (1 x 50) ]
[(49 x 50) = 2500 – 50 = 2450 ]

✨ Final Answers:

(a) (95 \times 8 = 760)
(b) (104 \times 15 = 1560)
(c) (49 \times 50 = 2450)

Is this quicker?

Yes ✅. This method is often quicker because:

Multiplying by round numbers (like 100, 50, 10) is easy.
Then you only need a small correction (adding or subtracting a simple product).
It reduces the need for long multiplication steps.

Question: Which other products might be quicker to find like the ones above?

Solution:

Excellent follow‑up 👌. The products that are quicker to calculate using this “nearby easy number” method are those where one factor is close to a round number (like 10, 50, 100, 1000) or has a simple multiple relationship.

✨ Examples of products that are quicker:

Close to 100
- (99 x 25 = (100 x 25) – (1 x 25) = 2475)
- (101 x 12 = (100 x 12) + (1 x 12) = 1212)
Close to 50
- (49 x 50 = (50 x 50) – (1 x 50) = 2450)
- (51 x 20 = (50 x 20) + (1 x 20) = 1020)
Close to 10 or multiples of 10
- (19 x 8 = (20 x 8) – (1 x 8) = 152)
- (21 x 15 = (20 x 15) + (1 x 15) = 315)
Close to 1000
- (999 x 7 = (1000 x 7) – (1 x 7) = 6993)
- (1001 x 25 = (1000 x 25) + (1 x 25) = 25,025)

🔑 General Rule

This shortcut works best when:

One number is just below or above a round number (like 10, 50, 100, 1000).
The other number is easy to multiply with that round number.
You can then add or subtract a small correction quickly.

✅ Student‑friendly takeaway:
Products like (99 x 25), (101 x 12), (49 x 50), (19 x 8), (999 x 7) are quicker to calculate mentally because they use nearby round numbers.

Figure it Out

Question 1. Fill in the blanks with numbers, and boxes by signs, so that the expressions on both sides are equal.

(a) 3 × (6 + 7) = 3 × 6 + 3 × 7

(b) (8 + 3) × 4 = 8 × 4 + 3 × 4

(d) (9 + 2) × 4 = 9 × 4 ☐ 2 ×______

(e) 3 × (_ + 4) = 3 +___

(f) (+ 6) × 4 = 13 × 4 +

(g) 3 × (+) = 3 × 5 + 3 × 2

(h) (+)×__= 2 × 4 + 3 × 4

(i) 5 × (9 – 2) = 5 × 9 – 5 × __

(j) (5 – 2) × 7 = 5 × 7 – 2 × __

(k) 5 × (8 – 3) = 5 × 8 ☐ 5 × __

(l) (8 – 3) × 7 = 8 × 7 ☐ 3 × 7

(m) 5 × (12 –) = ☐ 5 ×__

(n) (15 –) × 7 = ☐ 6 × 7

(o) 5 × (–) = 5 × 9 – 5 × 4

(p) (–) × __= 17 × 7 – 9 × 7

Solution:

This is a classic application of the distributive property of multiplication over addition. Let’s break it down:

(а) 3 × (6 + 7) = 3 × 6 + 3 × 7
(b) (8 + 3) × 4 = 8 × 4 + 3 × 4
(c) 3 × (5 + 8) = 3 × 5 + 3 × 8
(d) (9 + 2) × 4 = 9 × 4 + 2 × 4
(e) 3 × (10 + 4) = 30 + 12
(f) (13 + 6) × 4 = 13 × 4 + 24
(g) 3 × (5 + 2) = 3 × 5 + 3 × 2
(h) (2 + 3) × 4 = 2 × 4 + 3 × 4
(i) 5 × (9 – 2) = 5 × 9 – 5 × 2
(j) (5 – 2) × 7 = 5 × 7 – 2 × 7
(k) 5 × (8 – 3) = 5 × 8 – 5 × 3
(l) (8 – 3) × 7 = 8 × 7 – 3 × 7
(m) 5 × (12 – 3) = 60 – 5 × 3
(n) (15 – 6) × 7 = 105 – 6 × 7
(o) 5 × (9 – 4) = 5 × 9 – 5 × 4
(p) (17 – 9) × 7 = 17 × 7 – 9 × 7

Page 42

Question 2: In the boxes below, fill ‘<’, ‘>’ or ‘=’ after analysing the expressions on the LHS and RHS. Use reasoning and understanding of terms and brackets to figure this out and not by evaluating the expressions.

(a) (8 – 3) × 29 ▭ (3 – 8) × 29

(b) 15 + 9 × 18 ▭ (15 + 9) × 18

(d) (34 – 28) × 42 ▭ 34 × 42 – 28 × 42

Solution:

Perfect, let’s reason through each one carefully without direct calculation, just using properties of operations and brackets 👇

(a) ((8 – 3) × 29 ; ▭ ; (3 – 8) × 29)

(8 – 3 = +5) (positive)
(3 – 8 = -5) (negative)
Multiplying by the same 29, one side is positive, the other negative.
[ (8 – 3) × 29 > (3 – 8) × 29 ]
Answer: >

(b) (15 + 9 × 18 ; ▭ ; (15 + 9) × 18)

On the left, multiplication happens first: (9 × 18) then add 15.
On the right, bracket forces addition first: (15 + 9 = 24), then multiply by 18 (a much larger number).
So RHS is much larger.
[ 15 + 9 × 18 < (15 + 9) × 18 ]
Answer: <

(c) (23 × (17 – 9) ; ▭ ; 23 × 17 + 23 × 9)

LHS uses distributive property: (23 × (17 – 9) = 23 × 17 – 23 × 9).
RHS is (23 × 17 + 23 × 9).
Clearly, subtraction vs addition makes RHS larger.
[ 23 × (17 – 9) < 23 × 17 + 23 × 9 ]
Answer: <

(d) ((34 – 28) × 42 ; ▭ ; 34 × 42 – 28 × 42)

LHS: ((34 – 28) × 42 = 6 × 42).
RHS: distributive property: (34 × 42 – 28 × 42 = (34 – 28) × 42 = 6 × 42).
Both are exactly the same.
[ (34 – 28) × 42 = 34 × 42 – 28 × 42 ]
Answer: =

✅ Final Answers:
(a) >
(b) <
(c) <
(d) =

Question 3: Here is one way to make 14: 2 × ( 1 + 6 ) = 14. Are there other ways of getting 14? Fill them out below:

(a) _______ × ( ___+____) = 14

(b) _______ × ( ___+____) = 14

(d) _______ × ( ___+____) = 14

Solution:

Great question! We’re looking for different factorizations of 14 expressed in the form:

[ {number} x ({sum of two numbers}) = 14 ]

Step 1: Factorize 14

The factors of 14 are:

(1 x 14)
(2 x 7)
(7 x 2)
(14 x 1)

So we need to express the second factor as a sum of two numbers.

Step 2: Build expressions

(a) (2 x (3 + 4) = 2 x 7 = 14)

(b) (7 x (1 + 1) = 7 x 2 = 14)

(d) (1 x (7 + 7) = 1 x 14 = 14)

This shows how different factor pairs of 14 can be written in the form (a x (b + c)).

Question 4: Find out the sum of the numbers given in each picture below in at least two different ways. Describe how you solved it through expressions.

Solution:

Let’s look at each picture and add the numbers in two different reasoning-based ways, using expressions.

🟨🟦 Picture 1 (numbers 4 and 8)

What we see

It’s a 3 × 3 arrangement:

Five 4s
Four 8s

Way 1: Group by same numbers

[(5 x 4) + (4 \x 8)]

[= 20 + 32 = 52]

Way 2: Add row-wise

Each row adds up to:

Top row: (4 + 8 + 4 = 16)
Middle row: (8 + 4 + 8 = 20)
Bottom row: (4 + 8 + 4 = 16)

[16 + 20 + 16 = 52]

✅ Sum of Picture 1 = 52

🔵🔴 Picture 2 (numbers 5 and 6)

What we see

It’s a 4 × 4 arrangement:

Eight 5s
Eight 6s

Way 1: Group by same numbers

[(8 x 5) + (8 x 6)]

[= 40 + 48 = 88]

Way 2: Add row-wise

Each row:
[5 + 6 + 6 + 5 = 22]

There are 4 such rows:
[4 x 22 = 88]

✅ Sum of Picture 2 = 88

🌟 Key idea

You don’t need to add one number at a time.
You can:

Group equal numbers, or
Add row-wise or column-wise

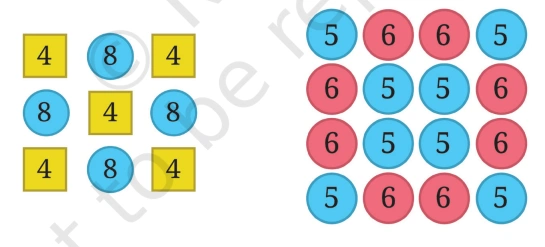
Both lead to the same total, just like rearranging terms in addition.

Page 42-43

Figure it Out

Question1: Read the situations given below. Write appropriate expressions for each of them and find their values.

(a) The district market in Begur operates on all seven days of a week. Rahim supplies 9 kg of mangoes each day from his orchard and Shyam supplies 11 kg of mangoes each day from his orchard to this market. Find the amount of mangoes supplied by them in a week to the local district market.

Solution:-

Step 1: Information given

Market operates 7 days a week.
Rahim supplies 9 kg per day.
Shyam supplies 11 kg per day.

Step 2: Expression for Rahim’s weekly supply

[ {Rahim’s supply in a week} = 9 x 7 = 63 kg ]

Step 3: Expression for Shyam’s weekly supply

[Shyam’s supply in a week = 11 x 7 = 77 kg ]

Step 4: Total supply together

[ Total supply = 63 + 77 = 140 kg ]

✅ Final Answer:

Rahim’s weekly supply = (9 x 7 = 63) kg
Shyam’s weekly supply = (11 x 7 = 77) kg
Total mangoes supplied in a week = 140 kg

(b) Binu earns ₹20,000 per month. She spends ₹5,000 on rent, ₹5,000 on food, and ₹2,000 on other expenses every month. What is the amount Binu will save by the end of a year?

Solution:-

Step 1: Monthly income

[ {Income per month} = ₹20,000 ]

Step 2: Monthly expenses

Rent = ₹5,000
Food = ₹5,000
Other expenses = ₹2,000

[ {Total expenses per month} = 5,000 + 5,000 + 2,000 = ₹12,000 ]

Step 3: Monthly savings

[ {Savings per month} = {Income} – {Expenses} = 20,000 – 12,000 = ₹8,000 ]

Step 4: Yearly savings

Since there are 12 months in a year:
[ {Savings in a year} = 8,000 x 12 = ₹96,000 ]

✅ Final Answer:
Binu will save ₹96,000 by the end of a year.

(c) During the daytime, a snail climbs 3 cm up a post, and during the night while asleep, accidentally slips down by 2 cm. The post is 10 cm high, and a delicious treat is on its top. In how many days will the snail get the treat?

Solution:-

Let’s carefully work this out step by step

Step 1: Net progress per day

Daytime climb = 3 cm
Nighttime slip = 2 cm
Net gain in one full day = (3 – 2 = 1) cm

So, after each complete day and night cycle, the snail is 1 cm higher.

Step 2: Think about the last climb

The post is 10 cm high.
If the snail only gains 1 cm per day, it seems like it would take 10 days.
But notice: on the final day, the snail climbs 3 cm and reaches the top before slipping back.

So we don’t count the slip on the last day.

Step 3: Calculate

After 7 full days (including slips), the snail will be at 7 cm.
On the 8th day, it climbs 3 cm straight to the top (7 + 3 = 10 cm).
It reaches the treat before slipping.

✅ Final Answer:
The snail will reach the treat in 8 days.

Question 2: Melvin reads a two-page story every day except on Tuesdays and Saturdays. How many stories would he complete reading in 8 weeks? Which of the expressions below describes this scenario?

(a) 5 × 2 × 8
(b) (7 – 2) × 8
(c) 8 × 7
(d) 7 × 2 × 8
(e) 7 × 5 – 2
(f) (7 + 2) × 8
(g) 7 × 8 – 2 × 8
(h) (7 – 5) × 8

Solution:

Let’s carefully solve this step by step

Step 1: Days Melvin reads in a week

There are 7 days in a week.
He does not read on Tuesdays and Saturdays → 2 days off.
So he reads on 7 – 2 = 5 days per week.

Step 2: Stories per week

Each day he reads 1 story (since each story is 2 pages, and he reads 2 pages daily).
So in 1 week, he completes 5 stories.

Step 3: Stories in 8 weeks

[ 5 x 8 = 40 {stories} ]

Step 4: Match with given expressions

Now check which expressions describe this scenario:

(a) (5 \times 2 \times 8 = 80) → ❌ (this counts pages, not stories)
(b) ((7 – 2) \times 8 = 5 \times 8 = 40) → ✅ correct
(c) (8 \times 7 = 56) → ❌ (all days, no off days)
(d) (7 \times 2 \times 8 = 112) → ❌ (pages, not stories, and all days)
(e) (7 \times 5 – 2 = 33) → ❌ incorrect reasoning
(f) ((7 + 2) \times 8 = 72) → ❌ wrong
(g) (7 \times 8 – 2 \times 8 = 56 – 16 = 40) → ✅ correct
(h) ((7 – 5) \times 8 = 2 \times 8 = 16) → ❌ wrong

✅ Final Answer:
Melvin completes 40 stories in 8 weeks.
The correct expressions are:

(b) (7 – 2) × 8
(g) 7 × 8 – 2 × 8

Question 3: Find different ways of evaluating the following expressions:

(a) 1 – 2 + 3 – 4 + 5 – 6 + 7 – 8 + 9 – 10
(b) 1 – 1 + 1 – 1 + 1 – 1 + 1 – 1 + 1 – 1

Solution:

Nice pattern-spotting problem. Let’s evaluate each in more than one way, mainly by grouping terms cleverly instead of straight calculation.

(a)

[1 – 2 + 3 – 4 + 5 – 6 + 7 – 8 + 9 – 10]

Way 1: Pair consecutive terms

Group each positive number with the negative number after it:

[(1 – 2) + (3 – 4) + (5 – 6) + (7 – 8) + (9 – 10)]

Each pair equals −1, so:

[-1 – 1 – 1 – 1 – 1 = {-5}]

Way 2: Group positives and negatives

Positives:
[1 + 3 + 5 + 7 + 9 = 25]

Negatives:
[2 + 4 + 6 + 8 + 10 = 30]

[25 – 30 = {-5}]

Way 3: Rearranging terms

Rearrange (addition allows this):

[(1 + 3 + 5 + 7 + 9) – (2 + 4 + 6 + 8 + 10)]

[= 25 – 30 = {-5}]

✅ Final value (a): −5

(b)

[1 – 1 + 1 – 1 + 1 – 1 + 1 – 1 + 1 – 1]

Way 1: Pair terms

[(1 – 1) + (1 – 1) + (1 – 1) + (1 – 1) + (1 – 1)]

Each pair is 0, so: Final Answer is [0]

Way 2: Count positives and negatives

Five +1
Five −1

They cancel each other:

[5 – 5 = 0]

Way 3: Rearrangement

[(1 + 1 + 1 + 1 + 1) – (1 + 1 + 1 + 1 + 1)]

[= 5 – 5 = {0}]

🌟 Key takeaway

Pairing and rearranging terms makes long expressions easy.
Equal numbers of + and − cancel out beautifully.

If you want, I can also show a general rule for sums like
(1 – 2 + 3 – 4 + ——–)

Question 4: Compare the following pairs of expressions using ‘<’, ‘>’ or ‘=’ or by reasoning.

(a) 49 – 7 + 8 ☐ 49 – 7 + 8
(b) 83 × 42 – 18 ☐ 83 × 40 – 18
(c) 145 – 17 × 8 ☐ 145 – 17 × 6
(d) 23 × 48 – 35 ☐ 23 × (48 – 35)
(e) (16 – 11) × 12 ☐ –11 × 12 + 16 × 12
(f) (76 – 53) × 88 ☐ 88 × (53 – 76)
(g) 25 × (42 + 16) ☐ 25 × (43 + 15)
(h) 36 × (28 – 16) ☐ 35 × (27 – 15)

Solution:

(a) 49 – 7 + 8 ☐ 49 – 7 + 8

Both sides are exactly the same expression.

✅ 49 – 7 + 8 = 49 – 7 + 8

(b) 83 × 42 – 18 ☐ 83 × 40 – 18

Left has 83 × 42
Right has 83 × 40

Since 42 > 40, the left product is bigger.
Both subtract 18, so the difference stays.

✅ 83 × 42 – 18 > 83 × 40 – 18

(c) 145 – 17 × 8 ☐ 145 – 17 × 6

(17 × 8 > 17 × 6)
A bigger number is being subtracted on the left

So the left side becomes smaller.

✅ 145 – 17 × 8 < 145 – 17 × 6

(d) 23 × 48 – 35 ☐ 23 × (48 – 35)

Left: subtract 35 after multiplying
Right: subtract 35 before multiplying

Subtracting before multiplying reduces the number much more.

So the left side is larger.

✅ 23 × 48 – 35 > 23 × (48 – 35)

(e) (16 – 11) × 12 ☐ –11 × 12 + 16 × 12

Right side can be rearranged:
[ 16 × 12 – 11 × 12 = (16 – 11) × 12 ]

Both sides are the same.

✅ (16 – 11) × 12 = –11 × 12 + 16 × 12

(f) (76 – 53) × 88 ☐ 88 × (53 – 76)

(76 – 53) is positive
(53 – 76) is negative

So:

Left is positive
Right is negative

✅ (76 – 53) × 88 > 88 × (53 – 76)

(g) 25 × (42 + 16) ☐ 25 × (43 + 15)

Inside brackets:

(42 + 16 = 58)
(43 + 15 = 58)

Same number multiplied by 25.

✅ 25 × (42 + 16) = 25 × (43 + 15)

(h) 36 × (28 – 16) ☐ 35 × (27 – 15)

(28 – 16 = 12)
(27 – 15 = 12)

Now compare:

Left: (36 × 12)
Right: (35 × 12)

Since 36 > 35, left is larger.

✅ 36 × (28 – 16) > 35 × (27 – 15)

Question 5: Identify which of the following expressions are equal to the given expression without computation. You may rewrite the expressions using terms or removing brackets. There can be more than one expression which is equal to the given expression.

(a) 83 – 37 – 12

(i) 84 – 38 – 12
(ii) 84 – (37 + 12)
(iii) 83 – 38 – 13
(iv) – 37 + 83 –12

(b) 93 + 37 × 44 + 76

(i) 37 + 93 × 44 + 76
(ii) 93 + 37 × 76 + 44
(iii) (93 + 37) × (44 + 76)
(iv) 37 × 44 + 93 + 76

Solution:

Let’s do this purely by structure and terms, not by calculating any values.

(a) Given expression

[83 – 37 – 12]

Rewrite it using terms:
[+83 -37 -12]

Now check each option.

(i) (84 – 38 – 12)

Terms are:
[+84 -38 -12]
Different numbers → not equal

❌

(ii) (84 – (37 + 12))

Removing brackets:
[+84 -37 -12]
The 83 has become 84, so terms differ.

❌

(iii) (83 – 38 – 13)

Terms:
[+83 -38 -13]
Different subtraction terms.

❌

(iv) (-37 + 83 – 12)

Reorder terms:
[+83 -37 -12]
Same terms, just rearranged.

✅ Equal

✅ Answer for (a): – [iv]

(b) Given expression

[93 + 37 x 44 + 76]

Key idea:

(37 x 44) is one term
Addition allows reordering, but multiplication structure must stay

(i) (37 + 93 x 44 + 76)

Here the multiplication is 93 × 44, not (37 × 44).

❌

(ii) (93 + 37 x 76 + 44)

Multiplication term has changed.

❌

(iii) ((93 + 37) x (44 + 76))

This changes addition into multiplication.

❌

(iv) (37 x 44 + 93 + 76)

Same terms, just reordered:
[37 x 44 +93 +76]

✅ Equal

✅ Final Answers

(a) → (iv)
(b) → (iv)

🔑 Rule to remember (exam gold)

You may reorder terms in addition
You may not change which numbers are multiplied
Brackets matter if they change signs or operations

Question 6: Choose a number and create ten different expressions having that value.

Solution:

Let me pick a nice, flexible number: 24 .
Now I’ll create ten different expressions that all have the value 24, using different operations and brackets.

Chosen number: 24

(20 + 4)
(30 – 6)
(6 x 4)
(48 ÷ 2)
((5 + 7) x 2)
(3 x (10 – 2))
(50 – (20 + 6))
(4 x (8 – 2))
((18 + 6))
((100 – 52))

What this shows

The same number can come from addition, subtraction, multiplication, division, or combinations.
Brackets help control the order without changing the final value.