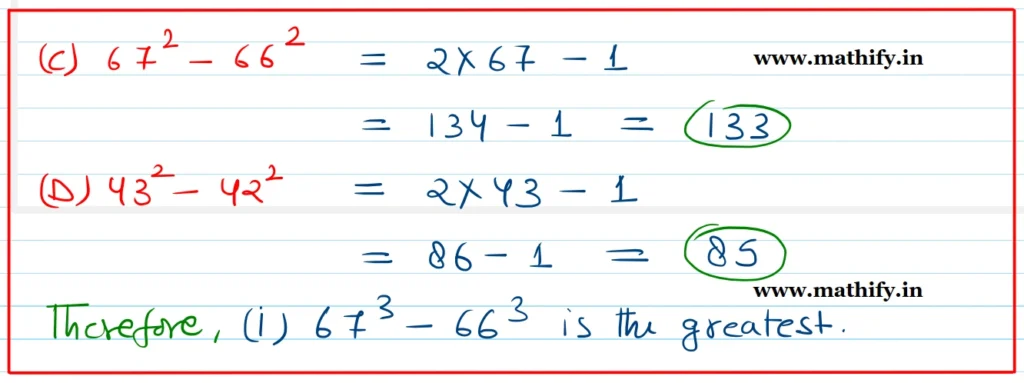NCERT Class 8 Solutions Chapter 1 A Square and a Cube Solutions (2025-26)
📘 NCERT Class 8 Maths Solutions – Ganita Prakash (New Editions) | 2025–26
Explore the latest NCERT Solutions for Class 8 Mathematics based on both old and new editions of the Ganita Prakash textbook, designed for the 2025–26 CBSE academic session. Available in Hindi and English Medium, these chapter-wise solutions include Multiple Choice Questions (MCQs) and detailed explanations to support exam preparation.
🔹 What’s Inside:
- Step-by-step solutions for all exercises in Algebra, Geometry, and Statistics
- Clear breakdowns of equations, formulas, and geometrical proofs
- Easy-to-understand methods aligned with CBSE guidelines
- Practice-ready MCQs for concept reinforcement
🔹 Why Students Love It:
- Makes complex topics simpler and more engaging
- Helps build strong conceptual clarity for CBSE Maths exams
- Ideal for self-study, revision, and classroom support
Whether you’re using the old Ganita Prakash edition or the new NCERT release, these solutions make Class 8 Maths accessible, exam-ready, and enjoyable.
NCERT Class 8 Maths Chapter 1 A Square and A Cube Solutions Question Answer
Ganita Prakash Class 8 Chapter 1 Solutions A Square and A Cube
NCERT Intext Questions Page (1 – 3)
Question – 1
Queen Ratnamanjuri had a will written that described her fortune of ratnas (precious stones) and also included a puzzle. Her son Khoisnam and their 99 relatives were invited to the reading of her will. She wanted to leave all of her ratnas to her son, but she knew that if she did so, all their relatives would pester Khoisnam forever. She hoped that she had
taught him everything he needed to know about solving puzzles. She left
the following note in her will—
“I have created a puzzle. If all 100 of you answer it at the same time, you will share the ratnas equally. However, if you are the first one to solve the problem, you will get to keep the entire inheritance to yourself. Good luck.” The minister took Khoisnam and his 99 relatives to a secret room in the mansion containing 100 lockers. The minister explained— “Each person is assigned a number from 1 to 100
Person 1 opens every locker.
- Person 2 toggles every 2nd locker (i.e., closes it if it is open, opens it if it is closed).
- Person 3 toggles every 3rd locker (3rd, 6th, 9th, … and so on).
- Person 4 toggles every 4th locker (4th, 8th, 12th, … and so on). This continues until all 100 get their turn.
In the end, only some lockers remain open. The open lockers reveal the code to the fortune in the safe.”
Q. Before the process begins, Khoisnam realises that he already knows which lockers will be open at the end. How did he figure out the answer?
Solution:-
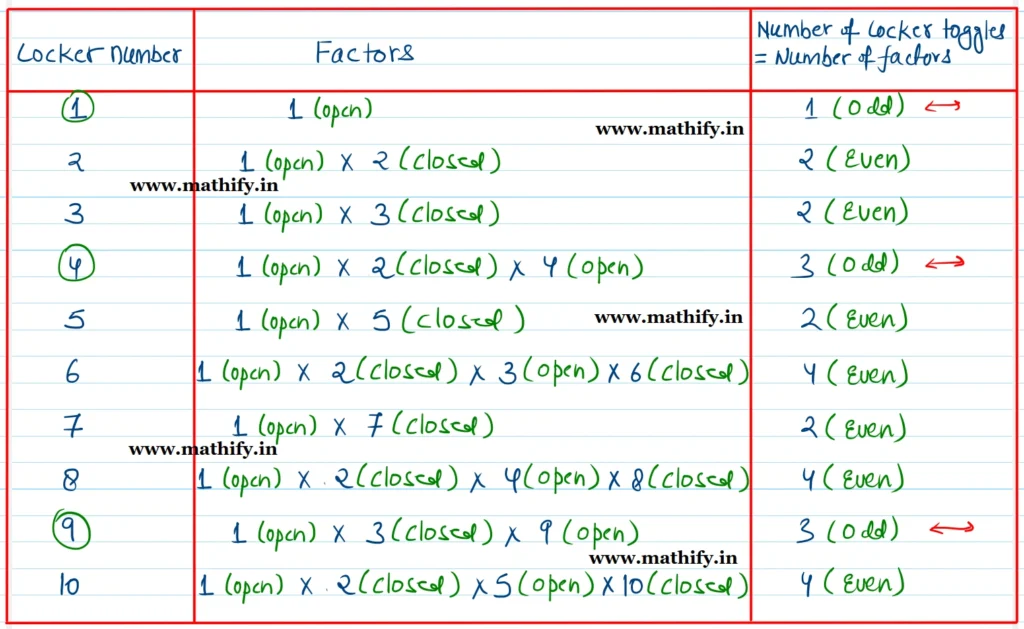
Khoisnam observed a clever mathematical pattern: each locker is toggled once for every person whose number is a factor of the locker’s number.
For Example: Locker number 6 is toggled by persons 1, 2, 3 and 6 and these are exactly the factors of number 6.
That means the total number of toggles a locker receives equals the number of its factors.
In similar way, locker number 5 is toggled by 1st and 5th person as the factor of 5 are 1, 5.
The locker number 8 is toggled by 1st, 2nd, 4th and 8th person as the factor of 8 are 1, 2, 4, 8.
Now here’s the twist—lockers toggled an even number of times end up closed, while those toggled an odd number of times stay open.
But only perfect squares have an odd number of factors, because one of their factors (like 6 in 36 = 6×6) repeats. So, at the end of the process, the lockers that remain open are precisely those numbered with perfect squares:
1, 4, 9, 16, 25, 36, 49, 64, 81, 100
These revealed the final code to the fortune.
It is more clarified by the table given below.
and so on for the other number upto 100.
Here in below table you can observe the other perfect squaure number from 16 to 100 all have odd factors numbers and remain open at the end.

Q. Does every number have an even number of factors?
Solution:-
Not all numbers have an even number of factors. In fact, only perfect squares have an odd number of factors. This happens because one of their factors is repeated — it’s the square root of the number. For example, in the case of 36, the factor 6 appears only once in the pair (6 × 6), making the total count of factors odd.
You can observe in below table

Q. Can you use this insight to find more numbers with an odd number of factors?
Solution:-

Q. Write the locker numbers that remain open.
Solution:-
10 lockers with perfect squares numbers will remain open are
= 1, 4, 9, 16, 25, 36, 49, 64, 81, 100
Q. Which are these five lockers?
Solutions:-
khoisnam immediately collects word clues from these 10 lockers and reads, “The passcode consists of the first five locker numbers that were touched exactly twice.”.
Thus the lockers that are toggled only twice must be the prime numbers since only the price number has only two factors the one is 1 and the second is number itself. So, the code is 2-3-5-7-11
You can observe this in in the table given below.

NCERT in-Text Questions – (4 – 5)
Patterns and Properties of Perfect Squares
Q. Find the squares of the first 30 natural numbers and fill in the table below.
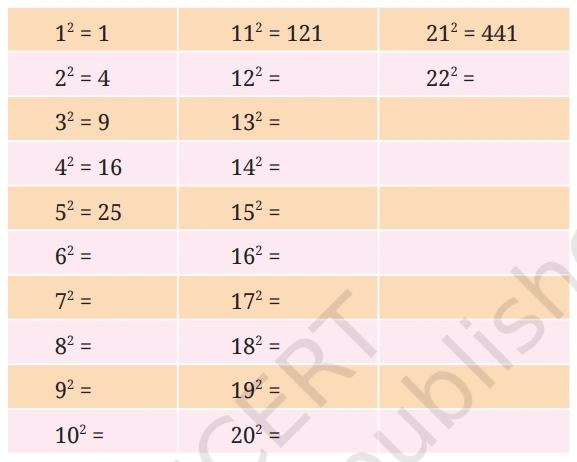
Solution:-
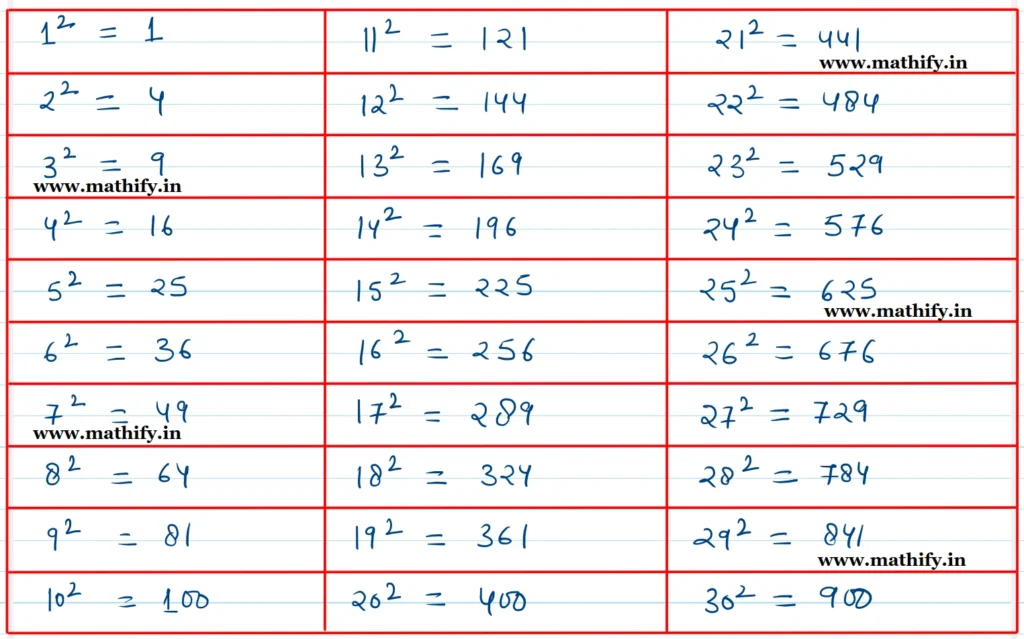
Question: What patterns do you notice? Share your observations and make conjectures.
Solution:-
By carfully observing the table it is observed that all perfect square numbers end with 0, 1, 4, 5, 6, or 9.
Thus the conclusion is if the numbers ends with 2, 3, 7 or 8 it is not a perfect squares and on the other hand if the number ends with 0, 1, 4, 5, 6 or 9, it is the perfect squere.
Question: If a number ends in 0, 1, 4, 5, 6 or 9, is it always a square?
Solution:-
🧠 Concept Check
Just because a number ends in 0, 1, 4, 5, 6, or 9, doesn’t mean it’s always a perfect square. These digits are common in square numbers, but not every number ending with them is a square.
But, the units digit can tell us when a number is not a square. If a number ends with 2, 3, 7, or 8, then we can definitely say that it is not a square.
📌 Why?
Perfect squares follow certain patterns, but they also have to meet other conditions — like having an exact square root. So we need to check more than just the last digit.
🔍 Examples to Understand
| Number | Ends in | Is it a Perfect Square? | Why? |
|---|---|---|---|
| 81 | 1 | ✅ Yes | √81 = 9 |
| 94 | 4 | ❌ No | √94 ≈ 9.7 (not whole) |
| 100 | 0 | ✅ Yes | √100 = 10 |
| 115 | 5 | ❌ No | √115 ≈ 10.7 |
| 36 | 6 | ✅ Yes | √36 = 6 |
| 129 | 9 | ❌ No | √129 ≈ 11.3 |
🧮 Conclusion for Students
👉 A number ending in 0, 1, 4, 5, 6 or 9 can be a square, but not always.
✅ To be sure, check if its square root is a whole number.
Question: Write 5 numbers such that you can determine by looking at their units digit that they are not squares.
Solution:-
🔍 Numbers That Cannot Be Perfect Squares (Based on Units Digit)
Some digits never appear at the end of a perfect square. If a number ends in these digits, it cannot be a square.
❌ Digits that never appear at the end of a square number:
2, 3, 7, or 8
📘 Examples of such numbers:
| Number | Units Digit | Reason It’s Not a Square |
|---|---|---|
| 23 | 3 | No square ends in 3 |
| 58 | 8 | No square ends in 8 |
| 97 | 7 | No square ends in 7 |
| 42 | 2 | No square ends in 2 |
| 103 | 3 | No square ends in 3 |
🧠 Quick Tip for Students:
If a number ends in 2, 3, 7, or 8, you can be sure it’s not a perfect square — no need to check the square root!
NCERT In-Text Question Page 5
Question: Which of the following numbers have the digit 6 in the units place?
(i) 382 (ii) 342 (iii) 462 (iv) 562 (v) 742 (vi) 822
Solution:-
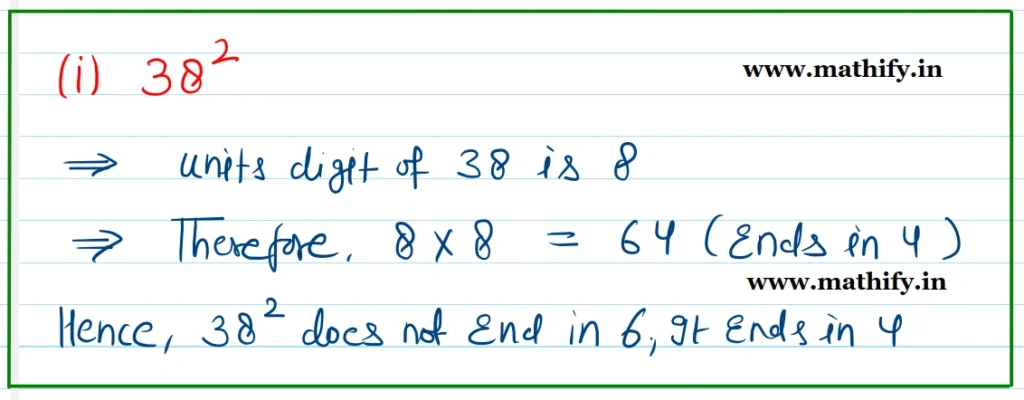
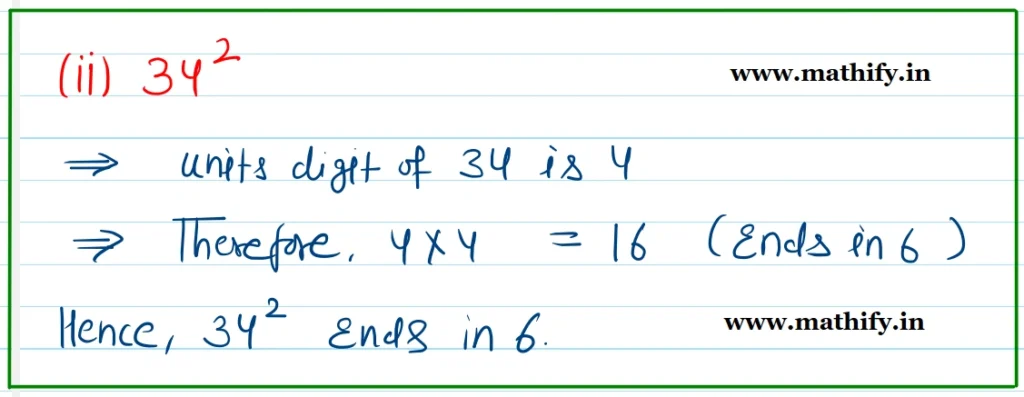
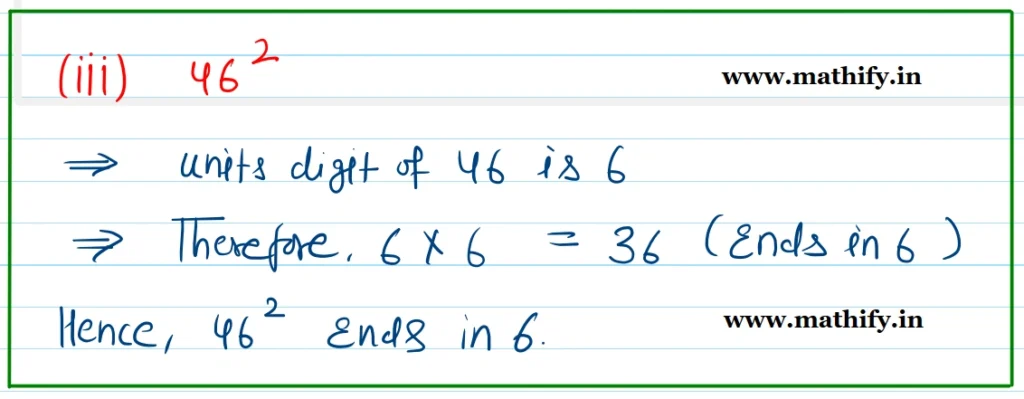
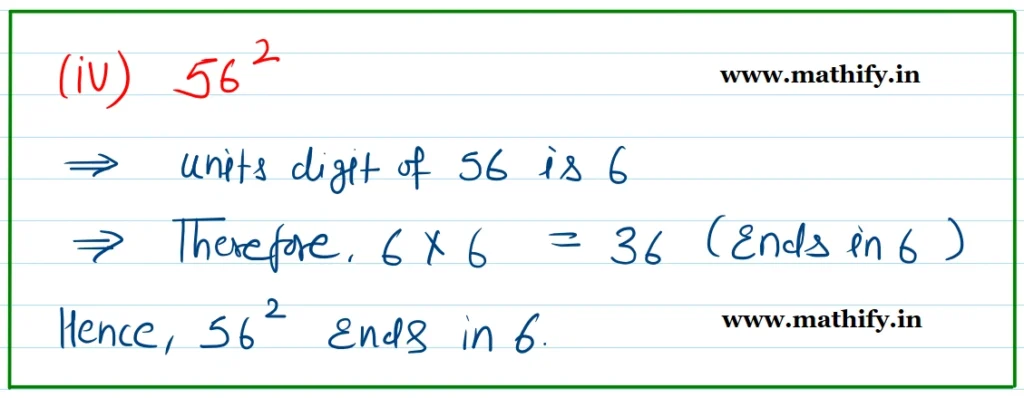
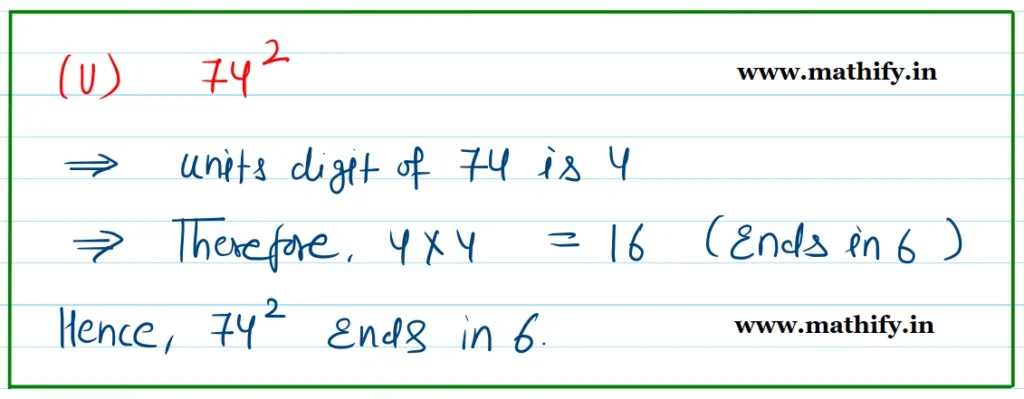
Question: Find more such patterns by observing the numbers and their squares from the table you filled earlier.
🔢 Unit Digit Pattern in Square Numbers
| Unit Digit of Number | Unit Digit of Its Square | Example |
|---|---|---|
| 0 | 0 | ( 102 = 100 ) |
| 1 | 1 | ( 112 = 121 ) |
| 2 | 4 | ( 122 = 144 ) |
| 3 | 9 | ( 132 = 169 ) |
| 4 | 6 | ( 142 = 196 ) |
| 5 | 5 | ( 152 = 225 ) |
| 6 | 6 | ( 162 = 256 ) |
| 7 | 9 | ( 172 = 289 ) |
| 8 | 4 | ( 182 = 324 ) |
| 9 | 1 | ( 192 = 361 ) |
Question: Consider the following numbers and their squares.
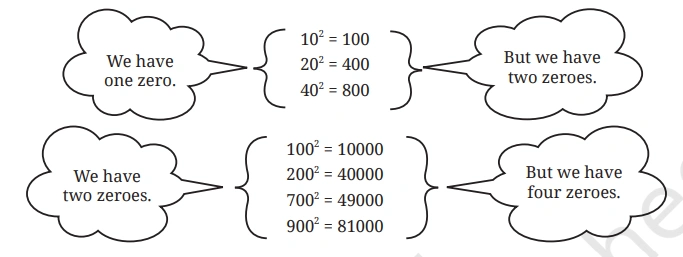
If a number contains 3 zeros at the end, how many zeros will its square have at the end?
Solution:-
The number of zeros at the end of the square of a number is always double the number of zeros at the end of the original number. Therefore, if a number contains 3 zeros at the end, then its squre will have 6 zeros.
Question: What do you notice about the number of zeros at the end of a number and the number of zeros at the end of its square? Will this always happen? Can we say that squares can only have an even number of zeros at the end?
Solution:
🧮 What Happens to Zeros When a Number Is Squared?
- If a number ends with zeros, its square will end with double the number of zeros.
- For example:
( 100 ) ends with 2 zeros → ( 1002 = 10,000 ) ends with 4 zeros
✅ Will This Always Happen?
Yes! Because squaring a number multiplies all its factors, including the 10s (which give zeros).
🔢 Can a Square Number Have Odd Number of Zeros?
No.
Square numbers always have even number of zeros at the end. That’s because squaring doubles the number of zeros.
Question: What can you say about the parity of a number and its square?
Solution:
🔢 What is Parity?
Parity means whether a number is even or odd.
✅ Parity of a Number and Its Square
- If a number is even, its square is also even.
👉 Example: ( 42 = 16 ) (both are even) - If a number is odd, its square is also odd.
👉 Example: ( 52 = 25 ) (both are odd)
So, the parity stays the same when you square a number.
🧠 Quick Tip for Students
Just look at the last digit:
- If it’s 0, 2, 4, 6, or 8 → even
- If it’s 1, 3, 5, 7, or 9 → odd
Squaring won’t change that!
NCERT In-Text Question Page (6-7)
Question: using the pattern above, find 362, given that 352 = 1225.
Solution:-

Question: Find how many numbers lie between two consecutive perfect squares. Do you notice a pattern?
Solution:-
🔢 How Many Numbers Lie Between Two Consecutive Perfect Squares?

✅ Examples
| n | ( n2 ) | ( (n+1)2 ) | Numbers Between | Count (2n) |
|---|---|---|---|---|
| 1 | 1 | 4 | 2, 3 | 2 |
| 2 | 4 | 9 | 5, 6, 7, 8 | 4 |
| 3 | 9 | 16 | 10 to 15 | 6 |
| 4 | 16 | 25 | 17 to 24 | 8 |
🧠 Pattern Noticed:
The number of values between two consecutive perfect squares is always even and increases by 2 each time.
Question: How many square numbers are there between 1 and 100? How many are between 101 and 200? Using the table of squares you filled earlier, enter the values below, tabulating the number of squares in each block of 100. What is the largest square less than 1000?
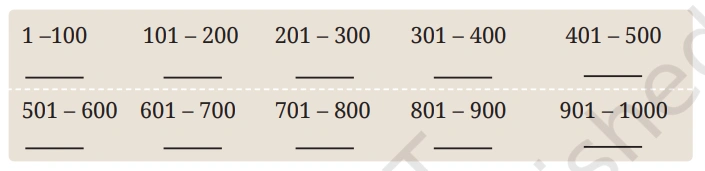
Solution:-
Here’s a clear and student-friendly breakdown for Class 7 CBSE learners, perfect for worksheets or blog content on Mathify.in:
📊 Square Numbers in Blocks of 100
Let’s list the square numbers and count how many fall in each 100-number block.
| Range | Square Numbers | Count |
|---|---|---|
| 1–100 | 1, 4, 9, 16, 25, 36, 49, 64, 81, 100 | 10 |
| 101–200 | 121, 144, 169, 196 | 4 |
| 201–300 | 225, 256, 289 | 3 |
| 301–400 | 324, 361, 400 | 3 |
| 401–500 | 441, 484 | 2 |
| 501–600 | 529, 576 | 2 |
| 601–700 | 625, 676 | 2 |
| 701–800 | 729, 784 | 2 |
| 801–900 | 841, 900 | 2 |
| 901–1000 | 961 | 1 |
✅ Largest Square Less Than 1000
The largest square number less than 1000 is:
[ 312 = 961]
NCERT In-Text Question Page (7, 8, 9)
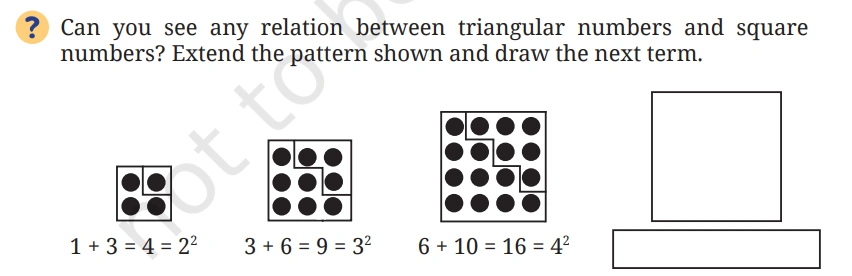
Solution:-
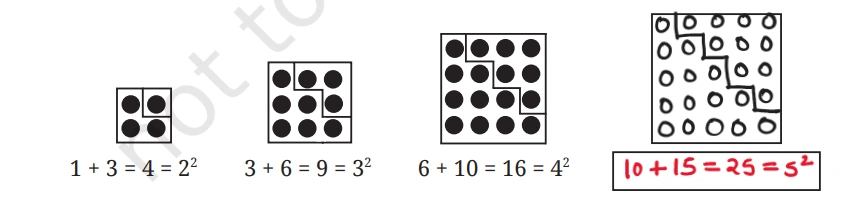

Solution:-


NCERT In-Text Question Page (10 – 11)
Figure it Out
Question 1: Which of the following numbers are not perfect squares?
(i) 2032 (ii) 2048 (iii) 1027 (iv) 1089
Solution:-

Question 2: Which one among 642, 1082, 2922, 362 has last digit 4?
Solution:-


Therefore, 1082 and 2922 have 4 as their last digits.
Question 3: Given 1252 = 15625, what is the value of 1262 ?
(i) 15625 + 126
(ii) 15625 + 262
(iii) 15625 + 253
(iv) 15625 + 251
(v) 15625 + 512
Solution:-


Question 4: Find the length of the side of a square whose area is 441 m2.
Solution:-

Question 5: Find the smallest square number that is divisible by each of the
following numbers: 4, 9, and 10.
Solution:-

Question 6: Find the smallest number by which 9408 must be multiplied so that
the product is a perfect square. Find the square root of the product.
Solution:-

Question7: How many numbers lie between the squares of the following numbers?
(i) 16 and 17 (ii) 99 and 100


Solution:-
Question 8: In the following pattern, fill in the missing numbers:
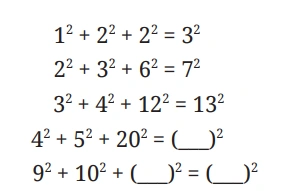
Solution:-

Question 9: How many tiny squares are there in the following picture? Write the prime factorisation of the number of tiny squares.

Solution:-

NCERT In-Text Questions Page (16 – 17)
Figure It Out
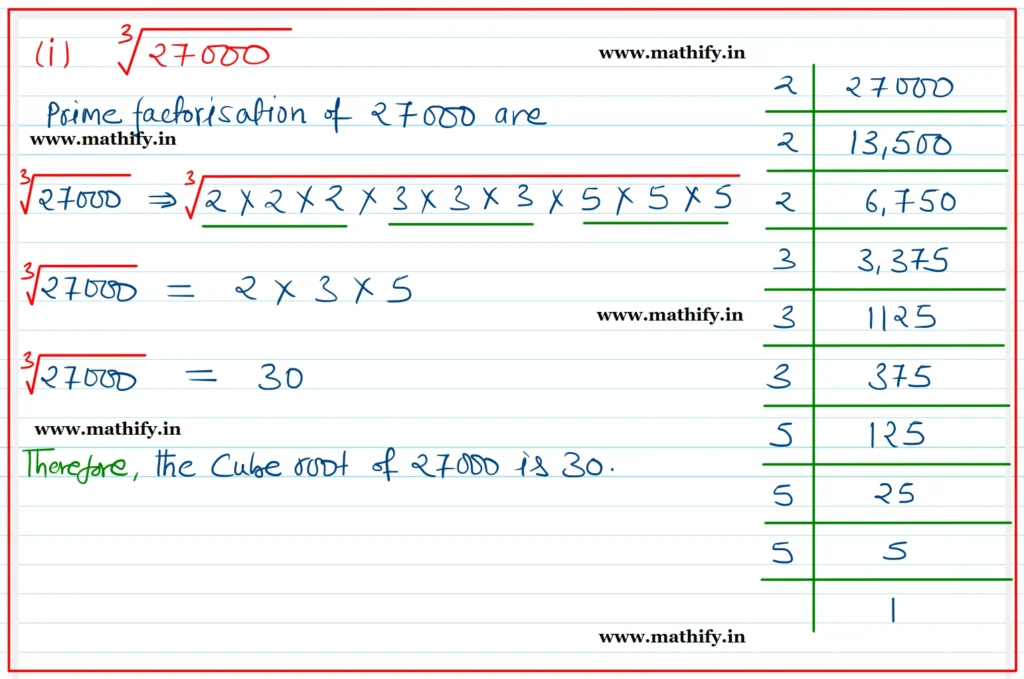
Question 1: Find the cube roots of 27000 and 10648.
Solution:-

Question 2: What number will you multiply by 1323 to make it a cube number?
Solution:-

Question 3: State true or false. Explain your reasoning.
(i) The cube of any odd number is even.
(ii) There is no perfect cube that ends with 8.
(iii) The cube of a 2-digit number may be a 3-digit number.
(iv) The cube of a 2-digit number may have seven or more digits.
(v) Cube numbers have an odd number of factors.
Solution:-
(i) The cube of any odd number is even. (False)
Reason: The cube of an odd number is always add, for example
⇨ 33 = 27
⇨ 53 = 125
⇨ 73 = 343
(ii) There is no perfect cube that ends with 8. (False)
Reason: The cubes of all the numbers ending with 2 at the unit place end ith 8.
⇨ 23 = 8
⇨ 123 = 1728
⇨ 223 = 10648
(iii) The cube of a 2 digit number may be a 3 digit number. (False)
Reason: Cube of a 2 digit number may have a minimum of 4 digits to a maximum of 6 digits.
For Example: 10 is the smallest 2 digit number, and 103 = 1,000, which has 4 digits.
(iv) The cube of a 2 digit number may have seven or more digits. (False)
Reason: Cube of a 2 digit number may have at most 6 digits.
For example: 99 is the largest 2 digit number and 993 = 970299, which is a 6 digit number.
(v) Cube numbers have an odd number of factors. (False)
Reason: Cube numbers may have an odd as wellas an even number of factors.
For example: 27 = 3 x 3 x 3 (odd number of factors)
= 64 = 2 x 2 x 2 x 2 x 2 x 2 (even number of factors)
Question 4: You are told that 1331 is a perfect cube. Can you guess without factorisation what its cube root is? Similarly, guess the cube roots of 4913, 12167, and 32768.
Solution:-
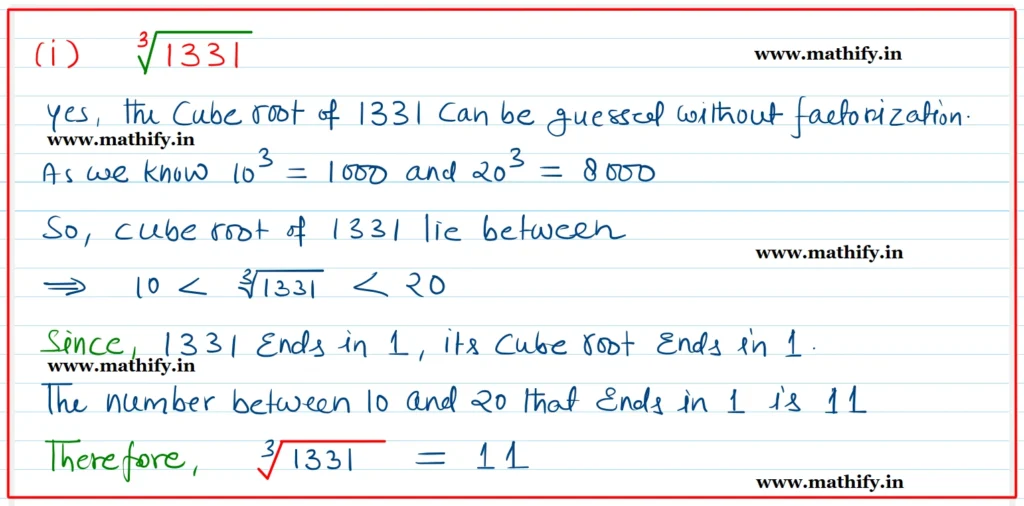

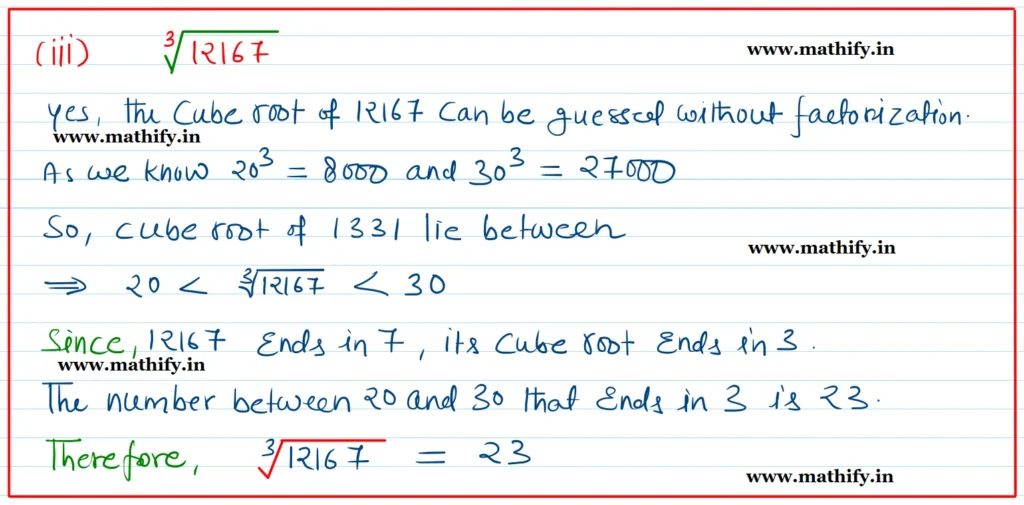

Question 5: Which of the following is the greatest? Explain your reasoning.
(i) 673 – 663
(ii) 433 – 423
(iii) 672 – 662
(iv) 432 – 422
Solution:-