A Story of Numbers Class 8 Solutions Ganita Prakash Maths Chapter 3
NCERT Solutions for Class 8 Maths Chapter 3 – A Story of Numbers (2025–26 Edition)
Explore the fascinating journey of numbers with our expertly crafted NCERT Solutions for Class 8 Maths Chapter 3 Ganita Prakash – A Story of Numbers. Aligned with the latest CBSE syllabus for the 2025–26 academic session, these solutions offer clear, step-by-step explanations that decode ancient number systems and cultural counting methods.
🔢 Key Concepts Covered:
- Evolution of number systems across civilizations
- Understanding base systems and place value
- Roman and Egyptian numerals explained
- Comparative reasoning across historical contexts
🧠 Why These Solutions Matter: Designed to spark mathematical curiosity, this chapter blends historical insights with logical reasoning. Through engaging activities and structured examples, students build a strong foundation in number sense and analytical thinking.
📘 Perfect for:
- CBSE Class 8 students seeking clarity and conceptual depth
- Teachers and parents supporting exam-readiness
- Learners curious about the origins and evolution of mathematics
NCERT In-Text Question Page 54
Reema’s Curosity
Figure it Out
Question 1: Suppose you are using the number system that uses sticks to represent numbers, as in Method 1. Without using either the number names or the numerals of the Hindu number system, give a method for adding, subtracting, multiplying and dividing two numbers or two collections of sticks.
Solution:
Question 2: One way of extending the number system in Method 2 is by using strings with more than one letter—for example, we could use ‘aa’ for 27. How can you extend this system to represent all the numbers? There are many ways of doing it!
Solution:
Question 3: Try making your own number system.
Solution:
NCERT In-Text Question Page 59
3.2 Some Early Number Systems
Figure it Out
Question: Represent the following numbers in the Roman system.
(i) 1222
(ii) 2999
(iii) 302
(iv) 715
Solution:-
NCERT In-Text Question Page (60-61)
Figure it Out
Question : A group of indigenous people in a Pacific island use different sequences of number names to count different objects. Why do you think they do this?
Solution:
Question 2: Consider the extension of the Gumulgal number system beyond 6 in the same way of counting by 2s. Come up with ways of performing the different arithmetic operations (+, –, ×, ÷) for numbers occurring in this system, without using Hindu numerals. Use this to evaluate the following:
(i) (ukasar-ukasar-ukasar-ukasar-urapon) + (ukasar-ukasarukasar-urapon)
(ii) (ukasar-ukasar-ukasar-ukasar-urapon) – (ukasar-ukasarukasar)
(iii) (ukasar-ukasar-ukasar-ukasar-urapon) × (ukasar-ukasar)
(iv) (ukasar-ukasar-ukasar-ukasar-ukasar-ukasar-ukasar-ukasar) ÷ (ukasar-ukasar)
Solution:
Question 3: Identify the features of the Hindu number system that make it efficient when compared to the Roman number system.
Solution:
Question 4: Using the ideas discussed in this section, try refining the number system you might have made earlier.
Solution:
NCERT In-Text Page (62)
3.3 The Idea of a Base
Figure it Out
Question 1: Represent the following numbers in the Egyptian system: 10458, 1023, 2660, 784, 1111, 70707.
Solution:
Question 2: What numbers do these numerals stand for?

Solution:
NCERT In-Text Page 63
Figure it Out
Question 1: Write the following numbers in the above base-5 system using the symbols in Table 2: 15, 50, 137, 293, 651.
Solution:
Question 2: Is there a number that cannot be represented in our base-5 system above? Why or why not?
Solution:
Question 3: Compute the landmark numbers of a base-7 system. In general, what are the landmark numbers of a base-n system? The landmark numbers of a base-n number system are the powers of n starting from n0 = 1, n, n2 , n3 ,…
Solution:
NCERT In-Text Question Page 65
Figure it Out
Question 1: Add the following Egyptian numerals:
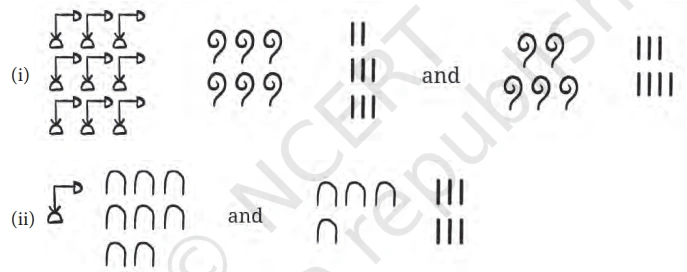
Solution:
Question 2: Add the following numerals that are in the base-5 system that we
created:

Solution:
NCERT In-Text Question Page 69-70
Figure it Out
Question 1: Can there be a number whose representation in Egyptian numerals has one of the symbols occurring 10 or more times? Why not?
Solution:
Question 2. Create your own number system of base 4, and represent numbers from 1 to 16.
Solution:
Question 3: Give a simple rule to multiply a given number by 5 in the base-5 system that we created.
Solution:
NCERT In-Text Question Page 73
Figure it Out
Question 1: Represent the following numbers in the Mesopotamian system —
(i) 63
(ii) 132
(iii) 200
(iv) 60
(v) 3605
Solution:
NCERT In-Text Question Page 73
Figure it Out
Question 1: Why do you think the Chinese alternated between the Zong and Heng symbols? If only the Zong symbols were to be used, how would 41 be represented? Could this numeral be interpreted in any other way if there is no significant space between two successive
positions?
Solution:
Question 2: Form a base-2 place value system using ‘ukasar’ and ‘urapon’ as the digits. Compare this system with that of the Gumulgal’s.
Solution:
Question 3: Where in your daily lives, and in which professions, do the Hindu numerals, and 0, play an important role? How might our lives have been different if our number system and 0 hadn’t been invented or conceived of?
Solution:
Question 4: The ancient Indians likely used base 10 for the Hindu number system because humans have 10 fingers, and so we can use our fingers to count. But what if we had only 8 fingers? How would we be writing numbers then? What would the Hindu numerals look like if we were using base 8 instead? Base 5? Try writing the base-10 Hindu numeral 25 as base-8 and base-5 Hindu numerals, respectively. Can you write it in base-2?
Solution: